Motivação e definições

Considere a matriz $A=\left[\begin{array}{cc} 1&2\\ 2&-2 \end{array}\right]$ . Para $b=\left[\begin{array}{c} 1\\ 0\end{array}\right]$ , obtemos $Ab=\left[\begin{array}{c}1\\ 2\end{array}\right]$ . Mas se tomarmos $c= \left[\begin{array}{c} 2\\ 1\end{array}\right]$ , temos que $Ac=2c$ . Ou seja, $Ac$ é um múltiplo de $c$ .

Dada uma matriz complexa $A$ quadrada, $n\times n$ , um vector $x\in {\mathbb{C}}^n$ não nulo diz-se um vector próprio de $A$ se $Ax=\lambda x$ , para algum $\lambda\in {\mathbb{C}}$ . O complexo $\lambda$ é denominado valor próprio, e dizemos que $x$ é vector próprio associado a $\lambda$ . O conjunto dos valores próprios de $A$ é denotado por $\sigma(A)$ e é chamado de espectro de $A$ .

No exemplo apresentado atrás, temos que $2\in \sigma(A)$ e que $\left[\begin{array}{c} 2\\ 1\end{array}\right]$ é vector próprio associado ao valor próprio 2.

Uma questão que colocamos desde já é:

Como encontrar $\sigma(A)$ ?

Ora, sendo $A$ uma matriz complexa $n\times n$ e se $\lambda$ é valor próprio de $A$ então existe $x\in {\mathbb{C}}^n\setminus \left\{0\right\}$ para o qual $Ax=\lambda x$ . Ou seja, $\lambda I_n x-Ax=\lambda x-Ax=0$ , o que equivale a $(\lambda I_n-A)x=0$ . Como $x\ne 0$ , tal significa que a equação $(\lambda I_n-A)x=0$ é consistente e que tem solução não nula. Isto é, a matriz quadrada $\lambda I_n-A$ tem característica estritamente inferior ao número de colunas, o que acontece se e só se não é invertível, ou de forma equivalente, o seu determinante é nulo. Os valores próprios de $A$ são os escalares $\lambda$ que tornam $\lambda I_n-A$ uma matriz singular, ou seja, que satisfazem $\vert\lambda I_n-A\vert=0$ . Ora $\vert\lambda I_n-A\vert$ é um polinómio em $\lambda$ , usando o teorema de Laplace, denominado polinómio característico de $A$ , e denotado por $\psi_A$ . Os valores próprios de $A$ são as raizes do polinómio característico $\psi_A$ , ou seja, as soluções da equação $\psi_A(\lambda)=0$ . Esta equação é chamada a equação característica de $A$ .

Determinar os valores próprios de uma matriz equivalente a determinar as raizes do seu polinómio característico. Usando o teorema de Laplace, este polinómio tem grau igual à ordem da matriz $A$ , que assumimos $n\times n$ , e é mónico: o coeficiente de $\lambda^n$ de $\psi_A(\lambda)$ é $1$ . Pelo Teorema Fundamental da Álgebra, sendo o grau de $\psi_A$ igual a $n$ este tem $n$ raizes (contando as suas multiplicidades) sobre ${\mathbb{C}}$ . Ou seja, a matriz $A$ do tipo $n\times n$ tem então $n$ valores próprios (contando com as suas multiplicidades). Sabendo que se $z\in {\mathbb{C}}$ é raiz de $\psi_A$ então o conjugado $\bar z$ de $z$ é raiz de $\psi_A$ , segue que se $\lambda\in \sigma(A)$ então $\bar \lambda \in \sigma(A)$ . Em particular, se $A$ tem um número ímpar de valores próprios (contado as suas multiplicidades) então tem pelo menos um valor próprio real. Isto é, $\sigma(A)\cap {\mathbb{R}}\ne \emptyset$ . A multiplicidade algébrica de um valor próprio $\lambda$ é a multiplicidade da raiz $\lambda$ de $\psi_A$ .

Vimos no que se discutiu acima uma forma de determinar os valores próprios de uma matriz. Dado um valor próprio $\lambda$ ,

Como determinar os vectores próprios associados a $\lambda\in \sigma(A)$ ?

Recorde que os vectores próprios associados a $\lambda\in \sigma(A)$ são as soluções não-nulas de $Ax=\lambda x$ , ou seja, as soluções não nulas de $(\lambda I_n-A)x=0$ . Isto é, os vectores próprios de $A$ associados a $\lambda$ são os elementos não nulos de $N(\lambda I_n -A)$ . Recorde que o núcleo de qualquer matriz é um espaço vectorial, e portanto $N(\lambda I_n -A)$ é o espaço vectorial dos vectores próprios de $A$ associados a $\lambda$ juntamente com o vector nulo, e denomina-se espaço próprio de $A$ associado a $\lambda$ . A multiplicidade geométrica de $\lambda$ é a dimensão do espaço próprio associado a $\lambda$ , isto é, $\dim N(\lambda I_n -A)$ .

O resultado seguinte resume o que foi afirmado na discussão anterior.

Teorema 4.1.1   Sejam $A$ uma matriz $n\times n$ e $\lambda\in {\mathbb{C}}$ . As afirmações seguintes são equivalentes:

1. $\lambda\in \sigma(A)$ ;
2. $(\lambda I_n-A)x=0$ é uma equação possível indeterminada;
3. $\exists_{x\in {\mathbb{C}}^n\setminus \left\{0\right\}} \, Ax=\lambda x$ ;
4. $\lambda$ é solução de $\vert\tilde\lambda I_n -A\vert=0$ .

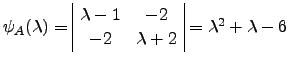Para a matriz considerada acima, $A=\left[\begin{array}{cc} 1&2\\ 2&-2 \end{array}\right]$ , o seu polinómio característico é $\psi_A(\lambda)=\begin{array}{\vert cc\vert} \lambda -1 & -2\\ -2 & \lambda +2\end{array}=\lambda^2+\lambda -6$ , cujas raizes são $-3,2$ . Portanto, $\sigma(A)=\left\{-3,2\right\}$ , e cada valor próprio de $A$ tem multiplicidade algébrica igual a 1.

Octave
Defina a matriz $A$ no Octave:

> A=[1 2; 2 -2]
A =

   1   2
   2  -2

Os coeficientes do polinómio característico de $A$ , por ordem decrescente do expoente de $\lambda$ , são obtidos assim:

> poly(A)
ans =

   1   1  -6

Ou seja, $\psi_A(\lambda)=\lambda^2+\lambda -6$ . As raizes de $\psi_A$ são os elementos de $\sigma(A)$ :

> roots (poly(A))
ans =

  -3
   2

A multiplicidade algbébrica de cada um deles é 1.

Os valores próprios de uma matriz dada são calculados de forma directa fazendo uso de

> eig(A)
ans =

  -3
   2

Resta-nos determinar vectores próprios associados a cada um destes valores próprios. Recorde que os vectores próprios associados a $-3$ [resp. 2] são os elementos não nulos de $N(-3I_2-A)$ [resp. $N(2I_2-A)$ ], pelo que nos basta pedir uma base para cada espaço próprio:

> null(-3*eye(2)-A)
ans =

   0.44721
  -0.89443

> null(2*eye(2)-A)
ans =

  0.89443
  0.44721

Ora a dimensão de cada um desses espaços vectoriais é 1, pelo que, neste caso, as multiplicidades algébrica e geométrica de cada um dos valores próprios são iguais. Mais adiante mostraremos uma forma mais expedita de obtermos estas informações.