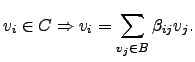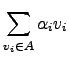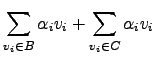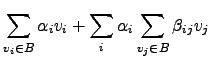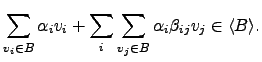Definição 3.3.1
Seja  um espaço vectorial.
Um conjunto
um espaço vectorial.
Um conjunto
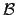 linearmente independente tal que
linearmente independente tal que
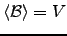 é chamado de base de
é chamado de base de  .
.
A demonstração do resultado que se segue envolve, no caso geral, diversos conceitos matemáticos (nomeadamente o Lema de Zorn) que ultrapassam em muito os propósitos desta disciplina. No entanto, o resultado garante, para qualquer espaço vectorial, a existência de um conjunto linearmente independente
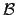 que gere o espaço vectorial.
que gere o espaço vectorial.
Teorema 3.3.2
Todo o espaço vectorial tem uma base.
Dizemos que  tem dimensão finita, ou que é finitamente gerado, se tiver uma base com um número finito de elementos. Caso contrário, diz-se que
tem dimensão finita, ou que é finitamente gerado, se tiver uma base com um número finito de elementos. Caso contrário, diz-se que  tem dimensão infinita.
tem dimensão infinita.
 tem dimensão finita nula se
tem dimensão finita nula se 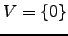 .
.
De ora em diante, apenas consideraremos espaços vectoriais finitamente gerados. Por vezes faremos referência à base
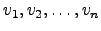 para indicar que estamos a considerar a base
para indicar que estamos a considerar a base
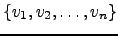 .
.
As coordenadas de 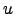 na base
na base
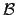 são denotadas3.2 por
são denotadas3.2 por
Recordemos que, se
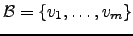 é uma base de
é uma base de  , em particular são linearmente independentes, e portanto dado
, em particular são linearmente independentes, e portanto dado 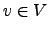 , os coeficientes de
, os coeficientes de 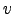 na base
na base
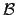 são únicos.
são únicos.
Teorema 3.3.4
Se um espaço vectorial tem uma base com um número finito 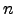 de elementos, então todas as bases de
de elementos, então todas as bases de  têm
têm 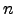 elementos.
elementos.
Seja  um espaço vectorial e
um espaço vectorial e
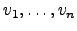 uma base de
uma base de  . Seja
. Seja
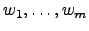 outra base de
outra base de  com
com 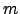 elementos.
elementos.
Como
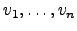 é base de
é base de  , existem
, existem
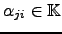 para os quais
para os quais
Note-se que
e que
Portanto,
é um sistema determinado, pelo que
Trocando os papéis de
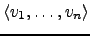 e de
e de
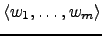 , obtemos
, obtemos 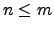 . Logo,
. Logo, 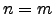 .
.
Definição 3.3.5
Seja  um espaço vectorial. Se existir uma base de
um espaço vectorial. Se existir uma base de  com
com 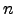 elementos, então diz-se que
elementos, então diz-se que  tem dimensão
tem dimensão 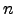 , e escreve-se
, e escreve-se
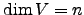 .
.
Corolário 3.3.6
Seja  um espaço vectorial com
um espaço vectorial com 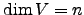 . Para
. Para 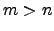 , qualquer conjunto de
, qualquer conjunto de 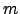 elementos de
elementos de  é linearmente dependente.
é linearmente dependente.
A demonstração segue da do teorema anterior.
Considerando o espaço vectorial
![$ {\mathbb{K}}_n[x]$](img762.png) dos polinómios com coeficientes em
dos polinómios com coeficientes em
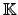 e grau não superior a
e grau não superior a 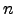 , uma base de
, uma base de
![$ {\mathbb{K}}_n[x]$](img762.png) é
é
De facto, qualquer polinómio de
![$ {\mathbb{K}}_n[x]$](img762.png) tem uma representação única na forma
tem uma representação única na forma
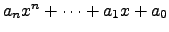 e portanto
e portanto 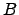 gera
gera
![$ {\mathbb{K}}_n[x]$](img762.png) , e
, e
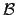 é linearmente independente. Logo,
é linearmente independente. Logo,
![$ \dim {\mathbb{K}}_n[x]=n+1$](img848.png) . Como exercício, mostre que
. Como exercício, mostre que
para um
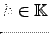 fixo, é outra base de
fixo, é outra base de
![$ {\mathbb{K}}_n[x]$](img762.png) .
.
Considere agora o conjunto
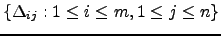 , onde
, onde
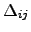 é a matriz
é a matriz 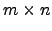 com as entradas todas nulas à excepção de
com as entradas todas nulas à excepção de 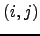 que vale 1. Este conjunto é uma base do espaço vectorial
que vale 1. Este conjunto é uma base do espaço vectorial
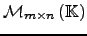 das matrizes
das matrizes 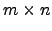 sobre
sobre
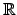 , pelo que
, pelo que
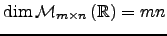 .
.
Teorema 3.3.7
Seja  um espaço vectorial com
um espaço vectorial com 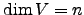 .
.
- Se
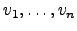 são linearmente independentes em
são linearmente independentes em  , então
, então
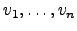 formam uma base de
formam uma base de  .
.
- Se
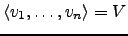 , então
, então
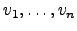 formam uma base de
formam uma base de  .
.
(1) Basta mostrar que
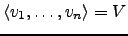 . Suponhamos, por absurdo, que
. Suponhamos, por absurdo, que
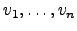 são linearmente independentes, e que
são linearmente independentes, e que
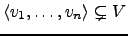 . Ou seja, existe
. Ou seja, existe
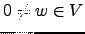 para o qual
para o qual
 . Logo,
. Logo,
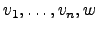 , são linearmente independentes, pelo que em
, são linearmente independentes, pelo que em  existem
existem 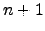 elementos linearmente independentes, o que contradiz o corolário anterior.
elementos linearmente independentes, o que contradiz o corolário anterior.
(2) Basta mostrar que
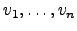 são linearmente independentes. Suponhamos que
são linearmente independentes. Suponhamos que
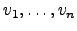 são linearmente dependentes e que
são linearmente dependentes e que
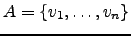 . Então pelo menos um deles é combinação linear dos outros. Ou seja, existe
. Então pelo menos um deles é combinação linear dos outros. Ou seja, existe 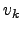 tal que
tal que
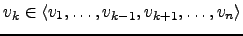 . Se
. Se
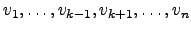 não forem linearmente independentes, então repetimos o processo até obtermos
não forem linearmente independentes, então repetimos o processo até obtermos
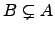 linearmente independente. Vamos mostrar que
linearmente independente. Vamos mostrar que
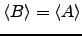 , recordando que
, recordando que
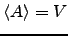 . Seja
. Seja
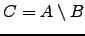 ; isto é,
; isto é, 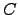 é o conjunto dos elementos que se retiraram a
é o conjunto dos elementos que se retiraram a 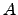 de forma a obter o conjunto linearmente independente
de forma a obter o conjunto linearmente independente 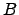 . Portanto,
. Portanto,
Seja então
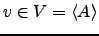 . Ou seja, existem
. Ou seja, existem 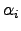 's para os quais
's para os quais
Portanto, 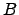 é uma base de
é uma base de  com
com 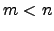 elementos, o que é absurdo.
elementos, o que é absurdo.
Corolário 3.3.8
Sejam  um espaço vectorial e
um espaço vectorial e 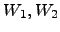 subespaços vectoriais de
subespaços vectoriais de  . Se
. Se
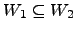 e
e
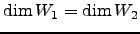 então
então 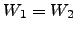
Se
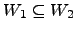 e ambos são subespaços de
e ambos são subespaços de  então
então 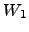 é subespaço de
é subespaço de 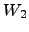 . Seja
. Seja
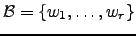 uma base de
uma base de 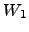 , com
, com
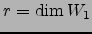 . Segue que
. Segue que
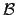 é linearmente independente em
é linearmente independente em 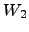 . Como
. Como
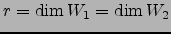 , temos um conjunto linearmente inpedente com
, temos um conjunto linearmente inpedente com 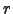 elementos. Por (1) do teorema,
elementos. Por (1) do teorema,
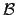 é base de
é base de 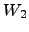 , o portanto
, o portanto
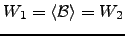 .
.
Corolário 3.3.9
Seja  um espaço vectorial e
um espaço vectorial e 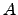 um conjunto tal que
um conjunto tal que
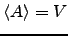 . Então existe
. Então existe
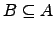 tal que
tal que 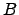 é base de
é base de  .
.
A demonstração segue o mesmo raciocínio da demonstração de (2) do teorema anterior.
pedro
2007-05-29
![]() que gere o espaço vectorial.
que gere o espaço vectorial.
![]() tem dimensão finita, ou que é finitamente gerado, se tiver uma base com um número finito de elementos. Caso contrário, diz-se que
tem dimensão finita, ou que é finitamente gerado, se tiver uma base com um número finito de elementos. Caso contrário, diz-se que ![]() tem dimensão infinita.
tem dimensão infinita.
![]() tem dimensão finita nula se
tem dimensão finita nula se ![]() .
.
![]() para indicar que estamos a considerar a base
para indicar que estamos a considerar a base
![]() .
.
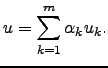
![$\displaystyle \left( u\right)_\mathcal{B}=\left[\begin{array}{c} \alpha_1\\ \alpha_2 \\ \vdots\\ \alpha_n\end{array}\right].$](img825.png)
![]() é uma base de
é uma base de ![]() , em particular são linearmente independentes, e portanto dado
, em particular são linearmente independentes, e portanto dado ![]() , os coeficientes de
, os coeficientes de ![]() na base
na base
![]() são únicos.
são únicos.
![]() é base de
é base de ![]() , existem
, existem
![]() para os quais
para os quais
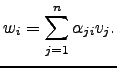
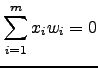
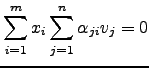
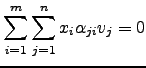
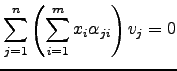
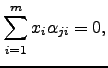 para todo
para todo ![$\displaystyle \left[\begin{array}{c} \alpha_{ji} \end{array}\right]\left[\begin{array}{c}x_1\\ \vdots\\ x_m \end{array}\right]= 0$](img837.png)
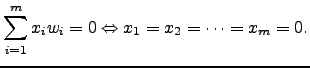
![$\displaystyle \left[\begin{array}{c} \alpha_{ji} \end{array}\right]\left[\begin{array}{c}x_1\\ \vdots\\ x_m \end{array}\right]= 0$](img837.png)
![$\displaystyle m = \mathrm{car}\left( \left[\begin{array}{c} \alpha_{ji} \end{array}\right]\right) \le n.$](img839.png)
![]() e de
e de
![]() , obtemos
, obtemos ![]() . Logo,
. Logo, ![]() .
.
![]() dos polinómios com coeficientes em
dos polinómios com coeficientes em
![]() e grau não superior a
e grau não superior a ![]() , uma base de
, uma base de
![]() é
é ![]() , onde
, onde
![]() é a matriz
é a matriz ![]() com as entradas todas nulas à excepção de
com as entradas todas nulas à excepção de ![]() que vale 1. Este conjunto é uma base do espaço vectorial
que vale 1. Este conjunto é uma base do espaço vectorial
![]() das matrizes
das matrizes ![]() sobre
sobre
![]() , pelo que
, pelo que
![]() .
.