Os grafos ![]() e
e ![]() são isomorfos,
são isomorfos,
![]() se exitir uma bijecção
se exitir uma bijecção
![]() tal que
tal que
![]() . Ou seja, existe uma bijecção entre o conjunto dos vértices dos dois grafos de tal forma que a incidência é preservada. Na prática, significa que se toma outra indexação para os vértices. Se
. Ou seja, existe uma bijecção entre o conjunto dos vértices dos dois grafos de tal forma que a incidência é preservada. Na prática, significa que se toma outra indexação para os vértices. Se ![]() for o isomorfismo, então escrever-se-á
for o isomorfismo, então escrever-se-á
![]() .
.
Dados dois grafos, uma forma possível de se testar o isomorfismo é percorrer todas as bijecções entre os dois conjuntos de vértices (repare que por (1) da proposição estes são necessariamente equipotentes) até se encontrar uma que preserva a vizinhança. Suponha que
![]() . Então existem
. Então existem ![]() bijecções possíveis, o que se para grafos com poucos vértices é realizável, torna-se num algoritmo pouco prático para outros grafos. Tal suscita o chamado Problema do Isomorfismo de Grafos, que pode ser exposto, de uma forma ingénua assim:
bijecções possíveis, o que se para grafos com poucos vértices é realizável, torna-se num algoritmo pouco prático para outros grafos. Tal suscita o chamado Problema do Isomorfismo de Grafos, que pode ser exposto, de uma forma ingénua assim:
Existem formas imediatas de teste de não isomorfismo, nomeadamente fazendo uso da proposição anterior. Em primeiro lugar, existe a condição de equipotência tratada nos pontos (1) e (2) da proposição. Por exemplo, não são isomorfos
![$\displaystyle \xymatrix{
& \bullet \ar@{-}[ld] \ar@{-}[rd] &\\
\bullet \ar@{-}...
...et } \hspace*{3cm}
\xymatrix{
\bullet \ar@{-}[r] & \bullet\ar@{-}[r]& \bullet}$](img98.png)
![$\displaystyle \xymatrix{
\bullet\ar@{-}[r] &\bullet\ar@{-}[r]\ar@{-}[d] &\bulle...
... &\bullet\ar@{-}[r]\ar@{-}[d] &\bullet\ar@{-}[r] &\bullet\\
& & \bullet & & }
$](img99.png)
Vejamos como se relacionam as matrizes de adjacência de dois grafos isomorfos. Para tal, dizemos que duas matrizes ![]() , quadradas com a mesma ordem, são permutacionalmente semelhantes,
, quadradas com a mesma ordem, são permutacionalmente semelhantes,
![]() , se existir uma matriz permutação
, se existir uma matriz permutação ![]() (ou seja, é obtida da matriz identidade fazendo trocas de linhas) tal que
(ou seja, é obtida da matriz identidade fazendo trocas de linhas) tal que ![]() .
.
Um grafo ![]() está contido num grafo
está contido num grafo ![]() ,
,
![]() , se
, se
![]() e
e
![]() .
.
![]() é subgrafo de
é subgrafo de ![]() se
se
![]() .
.
Um subgrafo
![]() de
de ![]() é gerador se
é gerador se
![]() . Ou seja, tem exactamente o mesmo conjunto de vértices.
. Ou seja, tem exactamente o mesmo conjunto de vértices.
Para
![]() , o subgrafo induzido por
, o subgrafo induzido por ![]() ,
,
![]() , é o subgrafo maximal
, é o subgrafo maximal
![]() de
de ![]() com
com
![]() . Este subgrafo é denotado por
. Este subgrafo é denotado por
![]() .
.
A proposição seguinte dá-nos outra forma de mostrar o não isomorfismo entre grafos (ou seja, fornece mais uma condição necessária do isomorfismo de grafos).
Mostremos o não isomorfismo entre os grafos seguintes, denotados respectivamente por ![]() e
e ![]() :
:
![$\displaystyle \xymatrix{
1 \ar@{-}[rrr] & & &2 \ar@{-}[ld] \ar@{-}[ddd]\\
& 5\...
...& h \ar@{-}[r]\ar@{-}[ld] & g \ar@{-}[rd]&\\
d \ar@{-}[rrr]\ar@{-}[uuu]& & &c}$](img119.png)
![$\displaystyle \xymatrix{
4 \ar@{-}[r] & 8 & 6\ar@{-}[r] &2}
\hspace*{3cm}
\xymatrix{
h\ar@{-}[d]\ar@{-}[r] & g\ar@{-}[d]\\
d\ar@{-}[r] & c}$](img126.png)
Um problema que se coloca é, de alguma forma, o recíproco da proposição. Por outras palavras, se certo tipo de subgrafos induzidos são isomorfos então serão os grafos isomorfos? Vejamos que tipo de subgrafos induzidos nos interessam.
Para
![]() ,
,
![]() é o subgrafo de
é o subgrafo de ![]() induzido por
induzido por
![]() .
Ou seja,
.
Ou seja,
![]() denota
denota
![]() . A lista de subgrafos de vértice eliminado é a representação dos subgrafos
. A lista de subgrafos de vértice eliminado é a representação dos subgrafos
![]() , onde
, onde ![]() percorre o conjunto dos vértices. Por exemplo, o grafo
percorre o conjunto dos vértices. Por exemplo, o grafo
![$\displaystyle \xymatrix{
& u \ar@{-}[ld] \ar@{-}[ldd]\ar@{-}[rdd] \ar@{-}[rd] & \\
y \ar@{-}[d] \ar@{-}[rrd] && v\ar@{-}[d]\ar@{-}[lld]\\
x \ar@{-}[rr] && w}$](img132.png)
![$ \xymatrix{
\bullet \ar@{-}[r]\ar@{-}[rd]\ar@{-}[d] & \bullet \ar@{-}[d]\\
\bullet\ar@{-}[r] & \bullet}$](img133.png) |
![$ \xymatrix{
\bullet \ar@{-}[r]\ar@{-}[d]\ar@{-}[rd] & \bullet \ar@{-}[d]\ar@{-}[ld]\\
\bullet\ar@{-}[r] & \bullet}$](img134.png) |
![$ \xymatrix{
\bullet \ar@{-}[r]\ar@{-}[d]\ar@{-}[rd] & \bullet \ar@{-}[d]\\
\bullet\ar@{-}[r] & \bullet}$](img135.png) |
![$ \xymatrix{
\bullet \ar@{-}[r]\ar@{-}[d]\ar@{-}[rd] & \bullet \ar@{-}[d]\\
\bullet\ar@{-}[r] & \bullet}$](img135.png) |
![$ \xymatrix{
\bullet \ar@{-}[r]\ar@{-}[d]\ar@{-}[rd] & \bullet \ar@{-}[d]\ar@{-}[ld]\\
\bullet\ar@{-}[r] & \bullet}$](img134.png) |
|
|
|
|
|
|
O Problema da Reconstrução do Grafo consiste em decidir se dois grafos não isomorfos com 3 ou mais vértices podem ter a mesma lista de subgrafos de vértice eliminado.
Acrescente-se que, de forma independente, em 1977 foi mostrado por B. McKay e por A. Nijenhuis, recorrendo a computadores, que um possível contra-exemplo da conjectura teria que ter, pelo menos, 10 vértices.
Recorde a definição de digrafo completo. Ao se considerarem grafos (ou seja, digrafos simétricos), a noção de grafo completo é a induzida pelo digrafo, com a nuance de se assumir que o digrafo é simples. Ou seja, um grafo simples (isto é, sem lacetes), diz-se completo de quaisquer dois vértices são vizinhos um do outro. Um ![]() -grafo completo é denotado por
-grafo completo é denotado por
![]() .
.
|
|
![$ \xymatrix{
& \ar@{-}[ld]\bullet \ar@{-}[rd] &\\
\bullet \ar@{-}[rr] && \bullet }$](img150.png) |
![$ \xymatrix{
& \bullet \ar@{-}[ldd] \ar@{-}[d] \ar@{-}[rdd]& \\
& \bullet\ar@{-}[ld]\ar@{-}[rd] & \\
\bullet \ar@{-}[rr] & & \bullet}$](img151.png) |
![$ \xymatrix{
& \bullet \ar@{-}[ld] \ar@{-}[ldd]\ar@{-}[rdd] \ar@{-}[rd] & \\
\b...
...ar@{-}[rrd] && \bullet\ar@{-}[d]\ar@{-}[lld]\\
\bullet \ar@{-}[rr] && \bullet}$](img152.png) |
|
|
|
|
|
|
|
Um bigrafo ou grafo bipartido
![]() é tal que
é tal que
![]() , com
, com
![]() mas
mas
![]() , e
, e
![]() . Ou seja, toda a aresta é incidente com um vértice de
. Ou seja, toda a aresta é incidente com um vértice de ![]() e um vértice de
e um vértice de ![]() . Portanto, existe uma partição do conjunto dos vértices de tal forma que dois vértices na mesma componente da partição não são vizinhos.
. Portanto, existe uma partição do conjunto dos vértices de tal forma que dois vértices na mesma componente da partição não são vizinhos.
Um bigrafo é completo se tiver todas as arestas possíveis incidentes com um vértice de ![]() e um de
e um de ![]() . De outra forma,
. De outra forma,
Se
![]() então com grafo bipartido completo com
então com grafo bipartido completo com
![]() como vértices denota-se por
como vértices denota-se por
![]() . Por exemplo,
. Por exemplo,
![$ \xymatrix{
\circ\ar@{-}[r]\ar@{-}[rd]\ar@{-}[rdd] & \bullet\\
\circ\ar@{-}[r...
...-}[r]\ar@{-}[rd] & \bullet\\
\circ\ar@{-}[ru] \ar@{-}[r]\ar@{-}[ruu]& \bullet}$](img171.png) |
![$ \xymatrix{ \circ\ar@{-}[r]\ar@{-}[rd]\ar@{-}[rdd] & \bullet\\
\circ\ar@{-}[ru] \ar@{-}[r]\ar@{-}[rd] & \bullet\\
& \bullet}$](img172.png) |
![$ \xymatrix{ \circ \ar@{-}[r]\ar@{-}[d] & \bullet\\
\bullet\ar@{-}[r] & \circ\ar@{-}[u]}$](img173.png) |
![$ \xymatrix{
& \circ \ar@{-}[d] & \\
\circ \ar@{-}[r] &\bullet\ar@{-}[r]\ar@{-}[d] &\circ\\
& \circ & }$](img174.png) |
|
|
|
|
|
O grafo bipartido completo
![]() chama-se, por razões óbvias, estrela.
chama-se, por razões óbvias, estrela.
Note-se que
![]() .
.
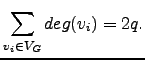
A demonstração é feita por indução sobre o número de arestas.
Prove-se o resultado para grafos ![]() . Ou seja, o grafo tem
. Ou seja, o grafo tem ![]() vértices e 1 aresta (
vértices e 1 aresta (![]() ). Tem-se então que existem apenas 2 vértices
). Tem-se então que existem apenas 2 vértices ![]() incidentes. Ou seja,
incidentes. Ou seja,
![]() e
e
![]() , para
, para ![]() . A igualdade do teorema de Euler é satisfeita de forma imediata.
. A igualdade do teorema de Euler é satisfeita de forma imediata.
Suponhamos agora que a igualdade é válida para grafos ![]() . Pretende-se que tal é suficiente para a validade da igualdade em grafos
. Pretende-se que tal é suficiente para a validade da igualdade em grafos ![]() . Seja, então,
. Seja, então, ![]() um grafo com
um grafo com ![]() vértices e
vértices e ![]() arestas. Sejam
arestas. Sejam ![]() uma aresta de
uma aresta de ![]() fixa arbitrariamente e
fixa arbitrariamente e
![]() . Ora
. Ora ![]() é um grafo
é um grafo ![]() , pelo que a hipótese de indução mostra que
, pelo que a hipótese de indução mostra que

Ao incluirmos a aresta ![]() , esta contribui com 2 unidades na soma total dos graus dos vértives de
, esta contribui com 2 unidades na soma total dos graus dos vértives de ![]() . Logo, e recordando que
. Logo, e recordando que
![]() ,
,
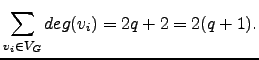
Dado ![]() um grafo simples
um grafo simples ![]() , então
, então
Se
![]() , então
, então
![]() . Neste caso, diz-se que o grafo é regular com grau
. Neste caso, diz-se que o grafo é regular com grau ![]() , ou que o grafo é
, ou que o grafo é ![]() -regular.
-regular.
Um grafo ![]() regular com
regular com ![]() chama-se um grafo cúbico.
chama-se um grafo cúbico.
Os grafos platónicos são os correspondentes2 aos cinco sólidos platónicos3. Saliente-se, no entanto, que um grafo cúbico não é necessariamente o cubo. Como exemplo, repare no grafo de Petersen:
![$\displaystyle \xymatrix{
& & \bullet \ar@{-}[lldd] \ar@{-}[d] \ar@{-}[rrdd] & &...
... \ar@{-}[ld] & & \bullet\ar@{-}[rd] &\\
\bullet \ar@{-}[rrrr] & & & &\bullet
}$](img205.png)