Códigos lineares

Os códigos de Hamming são códigos lineares em que a matriz de paridade pode ser dada por uma matriz de Hamming. Estes têm a vantagem de serem perfeitos, embora sejam apenas correctores de erros singulares e de os parâmetros seguirem regras (mais) fixas.

O esquema que se irá seguir de correcção de erros de códigos lineares gerais recorre aos síndromes. Para tal, é preciso calcular o número de erros do código linear à custa de, por exemplo, uma matriz geradora ou de uma matriz de paridade. Listam-se então os síndromes dos líderes de cada classe. Recebido um vector, este é corrigível se o seu síndrome igualar um único síndrome de um líderes, líder esse que é subtraído ao vector recebido por forma a se efectuar a correcção.

Suponha que $A$ é matriz geradora de um código $C$ , onde

$$A= \left(\begin{array}{ccccc} 1\,\text{mod}\,2 & 1\,\text{mod}\,2... ... & 1\,\text{mod}\,2 & 0\,\text{mod}\,2 \ & 1\,\text{mod}\,2\end{array}\right)$$

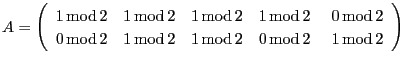
Esta matriz tem característica 2:

>> rank(A)
                                     2

Como o código é linear, a distância mínima do código é igual ao menor peso de Hamming das palavras-código não nulas. Ou seja, $d(C)=\min_{c\in C\setminus\{0\}} w(c)$ . As palavras código não nulas são as combinações lineares (não nulas) das linhas de $A$ . No nosso caso, row(A,1); row(A,2); row(A,1)+row(A,2). Segue que a distância mínima é $3$ , e portanto é corrector de erros singulares.

Para se aplicar o esquema de correcção de erros, é ainda necessário calcular a matriz de paridade. Ou seja, uma matriz com característica 3 tal que $AH^T=0$ . Ou ainda, uma matriz cujas colunas da transposta formem uma base do espaço nulo de $A$ .

>> nullspace(A)
             -- +-         -+  +-         -+  +-         -+ --
             |  |  0 mod 2  |  |  1 mod 2  |  |  1 mod 2  |  |
             |  |           |  |           |  |           |  |
             |  |  1 mod 2  |  |  0 mod 2  |  |  1 mod 2  |  |
             |  |           |  |           |  |           |  |
             |  |  1 mod 2  |, |  0 mod 2  |, |  0 mod 2  |  |
             |  |           |  |           |  |           |  |
             |  |  0 mod 2  |  |  1 mod 2  |  |  0 mod 2  |  |
             |  |           |  |           |  |           |  |
             |  |  0 mod 2  |  |  0 mod 2  |  |  1 mod 2  |  |
             -- +-         -+  +-         -+  +-         -+ --

Neste caso,

>> H:=concatMatrix(nullspace(A)[1],nullspace(A)[2],nullspace(A)[3])

                      +-                           -+
                      |  0 mod 2, 1 mod 2, 1 mod 2  |
                      |                             |
                      |  1 mod 2, 0 mod 2, 1 mod 2  |
                      |                             |
                      |  1 mod 2, 0 mod 2, 0 mod 2  |
                      |                             |
                      |  0 mod 2, 1 mod 2, 0 mod 2  |
                      |                             |
                      |  0 mod 2, 0 mod 2, 1 mod 2  |
                      +-                           -+

Em casos mais complexos, será preciso criar um ciclo de forma a se construir a concatenação iterativamente. Repare que a matriz de paridade é a transposta da matriz apresentada em cima. Portanto,

>> H:=transpose(H)
             +-                                             -+
             |  0 mod 2, 1 mod 2, 1 mod 2, 0 mod 2, 0 mod 2  |
             |                                               |
             |  1 mod 2, 0 mod 2, 0 mod 2, 1 mod 2, 0 mod 2  |
             |                                               |
             |  1 mod 2, 1 mod 2, 0 mod 2, 0 mod 2, 1 mod 2  |
             +-                                             -+

Os líderes são, visto o código corrigir 1 erro, as linhas da matriz identidade $I_5$ , e portanto os síndromes dos líderes não são mais que as colunas de $H$ .

Suponha que se recebeu por uma canal simétrico binário com ruído o vector

$$r= \left(\begin{array}{ccccc} 1\,\text{mod}\,2 & 0\,\text{mod}\,2 & 0\,\text{mod}\,2 & 1\,\text{mod}\,2 \ & 0\,\text{mod}\,2\end{array}\right)$$

Calcula-se o síndrome $Hr^T$ de $r$ :

>> H*transpose(r)
                               +-         -+
                               |  0 mod 2  |
                               |           |
                               |  0 mod 2  |
                               |           |
                               |  1 mod 2  |
                               +-         -+

Como o síndrome não é nulo, segue que $r\not\in C$ . Mas o síndrome de $r$ é igular à coluna 5 de $H$ , que por sua vez é o síndrome da linha $5$ de matriz identidade $I_5$ . Portanto, a correcção é feita como

>> I5:=M2(matrix::identity(5)):
>> c:=r+row(I5,5)
              +-                                           -+
              | 1 mod 2, 0 mod 2, 0 mod 2, 1 mod 2, 1 mod 2 |
              +-                                           -+