BCH

O código BCH é um código linear cíclico, construído à custa de polinómios sobre ${\mathbb{Z}}_2$ . O papel da primitividade de certos polinómios irredutíveis é crucial nesta teoria. Para tal, definamos o domínios dos polinómios sobre ${\mathbb{Z}}_2$ e teste-se a primitividade de $p(x)=x^4+x+1$ :

>> Pol2:=Dom::Polynomial(Dom::IntegerMod(2));
               Dom::Polynomial(Dom::IntegerMod(2), LexOrder)
>> q:=Pol2(x^4+x+1)
                             4
                  (1 mod 2) x  + (1 mod 2) x + (1 mod 2)
>> fs:=2^(degree(q))

                                    16
>> for i from 1 to fs-1 do
     field[i]:=powermod(x,i,q):
   end_for:

>> field[fs]:=0:
>> ftable:=table():
>> for i from 1 to fs-1 do
     ftable[field[i]]:=x^i:
   end_for:
>> ftable[field[fs]]:=0:
>> eval(ftable);

                         table(
                           0 = 0,
                                15
                           1 = x  ,
                            3        14
                           x  + 1 = x  ,
                            3    2        13
                           x  + x  + 1 = x  ,
                            3    2            12
                           x  + x  + x + 1 = x  ,
                            3    2        11
                           x  + x  + x = x  ,
                            2            10
                           x  + x + 1 = x  ,
                            3        9
                           x  + x = x ,
                            2        8
                           x  + 1 = x ,
                            3            7
                           x  + x + 1 = x ,
                            3    2    6
                           x  + x  = x ,
                            2        5
                           x  + x = x ,
                                    4
                           x + 1 = x ,
                            3    3
                           x  = x ,
                            2    2
                           x  = x ,
                           x = x
                         )

Vejamos como se pode escrever $x^3+1$ como elemento do grupo:

>> ftable[x^3+1]

                                     14
                                    x

Façamos agora uso do domínio dos corpos de Galois implementado no MuPAD:

p:=a^4+a+1:
F:=Dom::GaloisField(2,4,p):
PolF:=Dom::Polynomial(F)

Assuma $f(x)=x^{2^4-1}-1=x^{15}-1$ , e calcule-se a respectiva factorização em polinómios irredutíveis:

>> f:=Pol2(x^15-1)

                                    15
                         (1 mod 2) x   + (1 mod 2)
>> for i from 1 to (nops(factor(f))-1)/2 do
     print(factor(f)[2*i]);
   end_for;

                          (1 mod 2) x + (1 mod 2)

                             2
                  (1 mod 2) x  + (1 mod 2) x + (1 mod 2)

                             4              3
                  (1 mod 2) x  + (1 mod 2) x  + (1 mod 2)

                             4
                  (1 mod 2) x  + (1 mod 2) x + (1 mod 2)

                             4              3
                  (1 mod 2) x  + (1 mod 2) x  + (1 mod 2)

Construa-se uma tabela contendo os factores irredutíveis de $f(x)$ :

>> for i from 1 to (nops(factor(f))-1)/2 do
     TabFact[i]:=factor(f)[2*i]
   end_for:

Destes factores, vejamos de que potência de $\alpha$ são minimais aniquiladores:

for k from 1 to nops(TabFact) do  // vamos percorrer cada factor irredutivel
m:=TabFact[k]:
print("Polinomio: ",m,"  k=",k);  // mensagem de controlo
mF:=PolF(0):  // aqui comeca o algoritmo que transforma o polinomio em PolF
for i from 0 to degree(m) do
    mF:=mF+PolF(coeff(m,i)*x^i):
end_for:
for j from 1 to nops(solve(mF=0,x)) do
    print("solucoes: ",solve(mF=0,x)[j])  // agora temos as raizes sobre F
end_for
end_for

Uma rápida análise aos resultados, obtemos

>> m1:=TabFact[4]: m2:= m1: m4:=m1: m3:=TabFact[5]: m6:=m3: m5:=TabFact[2]:

onde m? indica o polinómio $m_i$ minimal aniquilador de $\alpha^i$ .

O caso menos evidente será a obtenção de $m_5$ . No entanto, fazendo

>> F(a^5)
                                   2
                                  a  + a

chega-se à conclusão que $x^5\equiv x^2+x$ , que por sua vez anula TabFact[2].

O polinómio do código BCH considerando as primeiras 6 potências de $\alpha$ é $g(x)=x^{10}+x^8+x^5+x^4+x^2+x+1$ :

>> g:=lcm(m1,m2,m3,m4,m5,m6)
           10              8              5              4
(1 mod 2) x   + (1 mod 2) x  + (1 mod 2) x  + (1 mod 2) x  +

              2
   (1 mod 2) x  + (1 mod 2) x + (1 mod 2)

A inserção de $g$ pode ser feita directamente:

>> g:=Pol2(x^10+x^8+x^5+x^4+x^2+x+1);
           10              8              5              4
(1 mod 2) x   + (1 mod 2) x  + (1 mod 2) x  + (1 mod 2) x  +
              2
   (1 mod 2) x  + (1 mod 2) x + (1 mod 2)

A codificação de um polinómio $h(x)$ é feita fazendo $h(x)g(x)$ . Por exemplo, para $h(x)=x^3+x+1$ ,

>> h:=Pol2(x^3+x+1)

                             3
                  (1 mod 2) x  + (1 mod 2) x + (1 mod 2)

>> Pol2(h*g)

           13              10              9              7
(1 mod 2) x   + (1 mod 2) x   + (1 mod 2) x  + (1 mod 2) x  +

              6              5
   (1 mod 2) x  + (1 mod 2) x  + (1 mod 2)

Assuma agora que foi recebido o polinómio $r(x)=1+x^2+x^3+x^4+x^5+x^6+x^7+x^{10}$ :

>> r:=Pol2(1+x^2+x^3+x^4+x^5+x^6+x^7+x^10)

           10              7              6              5
(1 mod 2) x   + (1 mod 2) x  + (1 mod 2) x  + (1 mod 2) x  +

              4              3              2
   (1 mod 2) x  + (1 mod 2) x  + (1 mod 2) x  + (1 mod 2)

O polinómio recebido não é palavra código, já que $g$ não divide $r$ :

>> Pol2(divide(r,g,Rem))

             8              7              6              3
  (1 mod 2) x  + (1 mod 2) x  + (1 mod 2) x  + (1 mod 2) x  + (1 mod 2) x

O passo seguinte envolve o cálculo dos síndromes de $r(x)$ . Para tal, iremos transformar $r$ num polinómio em ${\mathbb{F}}[x]$ .

>> rF:=PolF(0):
   for i from 0 to degree(r) do
       rF:=rF+PolF(coeff(r,i)*x^i):
   end_for:
>> print(rF);

                    10    7    6    5    4    3    2
                   x   + x  + x  + x  + x  + x  + x  + 1

Assumimos que $r$ tem 3 erros. A tabela dos síndromes é calculada assim:

t:=3; syn:=array(1..2*t):
for i from 1 to 2*t do
    syn[i]:=evalp(rF,x=F(a^i)):
end_for: 
print(syn):

e obtemos

  +- 3   3    2   3    2   3    2           2           3    2        -+
  | a , a  + a , a  + a , a  + a  + a + 1, a  + a + 1, a  + a  + a + 1 |
  +-                                                                  -+

O sistema de equações lineares que se obtem (v. aulas teóricas), que determina os coeficientes do polinómio localizador de erros $E(z)$ tem como matriz

$$\left(\begin{array}{ccc} a^3 & a^3 + a^2 & a^3 + a^2\\ a^3 + a^2... ... + a^2 + a + 1\\ a^3 + a^2 & a^3 + a^2 + a + 1 & a^2 + a + 1\end{array}\right)$$

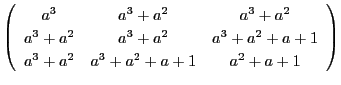
que resulta de

MatF:=Dom::Matrix(F)
V:=MatF([[syn[1],syn[2],syn[3]],[syn[2],syn[3],syn[4]],[syn[3],syn[4],syn[5]]])

O termo independente é

>> b:=MatF([[syn[4]],[syn[5]],[syn[6]]])

                           +-                 -+
                           |   3    2          |
                           |  a  + a  + a + 1  |
                           |                   |
                           |      2            |
                           |     a  + a + 1    |
                           |                   |
                           |   3    2          |
                           |  a  + a  + a + 1  |
                           +-                 -+

Verifique-se que a matriz é não-singular:

>> det(V)

                               3    2
                              a  + a  + a + 1

A única solucão é dada por $x=V^{-1}b$ :

>> inverseLU(V)

            +-                                               -+
            |       3    2       3    2           3    2      |
            |      a  + a ,     a  + a  + a + 1, a  + a  + 1  |
            |                                                 |
            |   3    2                               3        |
            |  a  + a  + a + 1,      a + 1,         a  + 1    |
            |                                                 |
            |     3    2              3           3    2      |
            |    a  + a  + 1,        a  + 1,     a  + a  + a  |
            +-                                               -+
>> solucao:=inverseLU(V)*b

                             +-             -+
                             |        2      |
                             |       a       |
                             |               |
                             |   3    2      |
                             |  a  + a  + 1  |
                             |               |
                             |        3      |
                             |       a       |
                             +-             -+

Vejamos a que potência de $\alpha$ corresponde a segunda entrada do vector solução:

>> ftable[x^3+x^2+1]

                                     13
                                    x

Temos então os síndromes, e portanto temos em nosso poder o polinómio localizador de erros $ELP$ :

sig2:=a^13
sig3:=a^3
sig1:=a^2
ELP:=x->x^3+sig3*x^2+sig2*x+sig

Por exaustão, encontram-se os zeros deste polinómio, e faz-se a correcção dos erros:

>> Erro:=Pol2(0):
>> for i from 0 to 14 do
       if F(ELP(a^i))=F(0) then
          print("erro na posicao ",i):
          Erro:=Erro+Pol2(x^i);
       end_if:
   end_for: print("e(x)=",Erro):

                           "erro na posicao ", 0

                           "erro na posicao ", 5

                          "erro na posicao ", 12

                                 12              5
             "e(x)=", (1 mod 2) x   + (1 mod 2) x  + (1 mod 2)
>> palavracod:=Pol2(r+Erro);

           12              10              7              6
(1 mod 2) x   + (1 mod 2) x   + (1 mod 2) x  + (1 mod 2) x  +

              4              3              2
   (1 mod 2) x  + (1 mod 2) x  + (1 mod 2) x