Códigos de Hamming

Os códigos de Hamming serão os primeiros com direito a implementação. No esquema de correcção de rros, será necessário escrever um número apresentado no sistema binário no decimal. De facto, o número será dado à custa de um vector (coluna) sobre ${\mathbb{Z}}_2$ . Por exemplo, o vector $[1,0,1,1]^T$ indica o número $(1011)_2$ . Pretende-se encontrar a representação decimal. Para tal, recordamos como se faz tal correspondência: a representação decimal de $(v_1v_2\cdots v_k)_2$ é

$$\sum_{i=1}^k v_i 2^{k-i}.$$

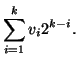
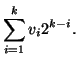
No exemplo anterior, temos $1\cdot 2^3+0\cdot 2^2 + 1\cdot 2^1 + 1\cdot 2^0$ , que no caso é 11. Este algoritmo é facilmente implementado.

No entanto, o vector $v$ fornecido pode ser elemento de ${\mathbb{Z}}_2$ .

>> Z2:=Dom::IntegerMod(2):
>> M2:=Dom::Matrix(Z2):
>> delete(i):
>> v:=M2([1,0,1,1]):
>> sum(v[i]*2^(4-i),i=1..4);

                                  1 mod 2

Aqui surge um problema, já que o MUPAD efectua os cálculos em ${\mathbb{Z}}_2$ .

Para contornar esta questão, transforma-se, à medida do necessário, as entradas $v[i]$ de $v$ dado em elementos de ${\mathbb{Z}}$ , fazendo uso de uma variável auxiliar:

>> aux:=coerce(v[i],Dom::Integer);

Assuma que usa um ciclo for. A cada passo do ciclo, a soma vai sendo calculada:

>> soma:=soma+aux*2^(n-i);

Ficamos, para este caso, com o ciclo seguinte:

>> soma:=0

                                     0
>> for i from 1 to 4 do
 aux:=coerce(v[i],Dom::Integer);
 soma:=soma+aux*2^(4-i);
 end_for: print(soma);

                                    11

Se estiver a construir um procedimento, não se esqueça de enviar o resultado para o programa principal:

return(soma);

Esta secção tem como finalidade fornecer algumas ideias para a implementação de um código de Hamming. Recorde que a correcção de erros de $r$ é feita à custa do síndrome de $r$ , ou seja, à custa do vector coluna $Hr^T$ , onde $H$ é a matriz de Hamming, matriz de paridade do código. Mais, um código de Hamming é um código perfeito corrector erros singulares. De facto, a posição do erro em $r$ é dada pela representação decimal de $Hr^T$ . Por exemplo, suponha que $r$ recebido tem síndrome $[1,0,1,1]^T$ . Pelo que foi visto nas aulas teóricas, a posição de $r$ com erro é $(1011)_2$ , que corresponde a $11$ na base 10. Note ainda que sendo $H$ a matriz de paridade do código de Hamming, com 4 linhas, então tem $2^4-1=15$ colunas. Ou seja, $r$ é um vector linha com 14 bits, sendo que o $11^\circ$ está incorrecto (segundo o esquema usado na correcção pelo vizinho mais próximo, fazendo uso da distância de Hamming).

É ainda necessário, de forma a se poder implementar um código de Hamming, construir um procedimento hamming:=proc(numero:Type::PosInt) onde $n$ é um argumento de entrada, número inteiro positivo, e cujo resultado final é uma matriz $n\times (2^n-1)$ , cuja coluna $j$ é a representação do número natural $j$ na sua escrita binária. Ou seja, uma forma fácil de construir uma matriz de Hamming. Para tal, concentramo-nos num algoritmo que, dado um número $(k)_{10}$ , encontre um vector coluna sobre ${\mathbb{Z}}_2$ , com dimensão fixa à partida, cujas entradas são os dígitos (0 ou 1) correspondentes à representação binária de $n$ . Por exemplo, que a $5$ , fixando em $4$ o número de linhas do vector, tenha como resultado $[0,1,0,1]^T$ .

Suponha, então, que se pretende construir um vector coluna $v$ , com dimen linhas, cujas entradas são os símbolos da representação binária de $q$ , onde dimen $\ge \lfloor\log_2 q\rfloor +1$ . Aplica-se o algoritmo da divisão:

$$q=q_0 = 2q_1+r_1,$$

$$q_1 = 2q_2+r_2,$$

$$\vdots$$

$$q_{n-2} = 2q_{n-1}+r_{n-1},$$

$$q_{n-1} = 2*0+r_n,$$

onde $0\le r_i<2$ . O vector pretendido será $[0,\dots,0,r_n,r_{n-1},\dots ,r_2,r_1]^T$ .

No que se segue, atribua 4 a dimen e 5 a $q$ .

>> for i from dimen downto 1 do
                v[i]:=Dom::IntegerMod(2)(q):
                q:=q div 2:
   end_for:
>> v;
                               +-         -+
                               |  0 mod 2  |
                               |           |
                               |  1 mod 2  |
                               |           |
                               |  0 mod 2  |
                               |           |
                               |  1 mod 2  |
                               +-         -+

O que lhe resta fazer? Construir cada coluna da matriz de Hamming, concatenando-as. Por exemplo:

export(linalg):
dimen:=3:
q:=1: v:=M2(dimen,1):
for i from dimen downto 1 do
                v[i]:=Dom::IntegerMod(2)(q):
                q:=q div 2:
   end_for:
H:=v:
for q2 from 2 to 2^dimen-1 do
q:=q2:for i from dimen downto 1 do
                v[i]:=Dom::IntegerMod(2)(q):
                q:=q div 2:
   end_for:
H:=concatMatrix(H,v)
end_for: print(H);

Suponha que foi recebido por uma canal simétrico binário

$$r=\left(\begin{array}{ccccccc} 1\,\text{mod}\,2 & 1\,\text{mod}\,... ...2 \ & 1\,\text{mod}\,2 & 1\,\text{mod}\,2 & 1\,\text{mod}\,2\end{array}\right)$$

onde o esquema de codificação usado foi Hamming [7,4]. Seja $H$ a matriz de Hamming com 3 linhas, que pode ser obtida pelas instruções atrás definidas. Basta-nos calcular o síndrome de $r$ , isto é, $Hr^T$ :

>> H*transpose(r)
                               +-         -+
                               |  0 mod 2  |
                               |           |
                               |  0 mod 2  |
                               |           |
                               |  0 mod 2  |
                               +-         -+

Assuma que previamente foi exportada a livraria linalg. Como o síndrome é o vector nulo, segue que $r$ é palavra-código.

Suponha agora que foi recebido

$$r=\left(\begin{array}{ccccccc} 1\,\text{mod}\,2 & 1\,\text{mod}\,... ... \ & 0\,\text{mod}\,2 & 0\,\text{mod}\,2 & 1\,\text{mod}\,2\end{array}\right)$$

Calcula-se o síndrome de $r$

>> s:=H*transpose(r)
                               +-         -+
                               |  1 mod 2  |
                               |           |
                               |  1 mod 2  |
                               |           |
                               |  1 mod 2  |
                               +-         -+

para se concluir que não é palavra-código. Sendo o código de Hamming, o processo de correcção de erros (neste caso de um erro) fornece um algoritmo para a correcção: o síndrome é a representação binária da posição de $r$ que tem o erro. Faça-se uso do que inicialmente se tratou nesta secção.

>> soma:=0:
for i from 1 to 3 do
 aux:=coerce(s[i],Dom::Integer);
 soma:=soma+aux*2^(3-i);
end_for: 
print(soma);
                                     7

Ou seja, o elemento $r[7]$ está errado. Corrijamo-lo:

>> r[soma]:=r[soma]+Z2(1);
                                  0 mod 2