-
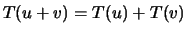 ;
;
-
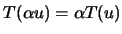 .
.
Para
![]() definidas por
definidas por
Apresentamos alguns exemplos clássicos de transformações lineares:
![]()
![]()
![]()
![]()
Seguinte: Propriedades das transformações lineares
Acima: Transformações lineares
Anterior: Transformações lineares
Conteúdo
Pedro Patricio
2008-01-08