-
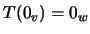 para
para
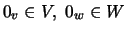 ;
;
-
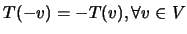 ;
;
-
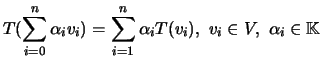 ;
;
- Se
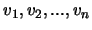 são vectores de
são vectores de  linearmente
dependentes, então
linearmente
dependentes, então
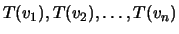 são vectores de
são vectores de
 linearmente dependentes.
linearmente dependentes.
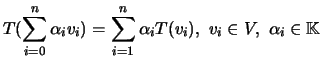 ;
;
Se
![]() são vectores de
são vectores de ![]() linearmente
dependentes então um deles, digamos
linearmente
dependentes então um deles, digamos ![]() , escreve-se como combinação linear dos restantes:
, escreve-se como combinação linear dos restantes:
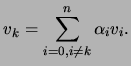
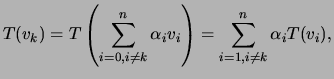
Em geral, uma transformação não preserva a independência linear. Por exemplo, a transformação linear
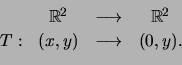
Recordamos que, apesar de indicarmos uma base como um conjunto de vectores, é importante a ordem pela qual estes são apresentados. Ou seja, uma base é um n-uplo de vectores. Por forma a não ser confundida por um n-uplo com entradas reais, optámos por indicar uma base como um conjunto. É preciso enfatizar esta incorrecção (propositadamente) cometida.
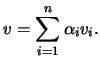
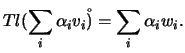
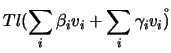 |
|||
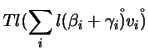 |
|||
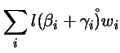 |
|||
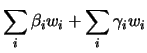 |
|||
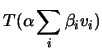 |
|||
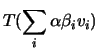 |
|||
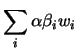 |
|||
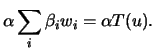 |
Mostre-se, agora, a unicidade. Suponhamos que ![]() é uma aplicação linear que satisfaz
é uma aplicação linear que satisfaz
![]() , para todo o
, para todo o ![]() no conjunto dos índices. Seja
no conjunto dos índices. Seja ![]() , com
, com
![]() . Então
. Então
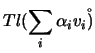 |
|||
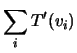 |
|||
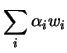 |
|||
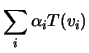 |
|||
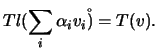 |
Seja
![]() uma base de
uma base de ![]() e
e ![]() um
vector qualquer de
um
vector qualquer de ![]() . Então
. Então
![]() .
Vamos definir uma transformação
.
Vamos definir uma transformação ![]() ,
,
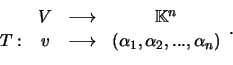
(a) A aplicação ![]() é bijectiva.
é bijectiva.
Primeiro, verificamos que ![]() é injectiva, i.e., que
é injectiva, i.e., que
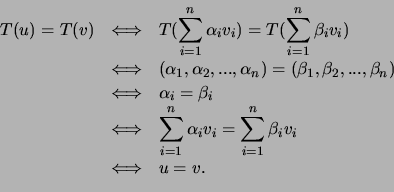
Mostramos, agora, que ![]() é sobrejectiva, i.e., que
é sobrejectiva, i.e., que
![]() é sobrejectiva
é sobrejectiva ![]()
(b) A aplicação ![]() é linear.
é linear.
Por exemplo, o espaço vectorial
![]() é isomorfo a
é isomorfo a
![]() . De facto, considerando a base de
. De facto, considerando a base de
![]()
![$\displaystyle \left[\begin{array}{ccc}1 & 0 & 0\\ 0 & 0 & 0\end{array}\right]
\...
...rray}\right],
\left[\begin{array}{ccc}0 & 0 & 0\\ 0 & 0 & 1\end{array}\right],$](img1407.png)
![$ \left[\begin{array}{ccc}a & b&c\\ d & e & f\end{array}\right]$](img1408.png) é o vector
é o vector
![$ T\left(\left[\begin{array}{ccc}a & b&c\\ d & e & f\end{array}\right]\right)=(a,b,c,d,e,f)$](img1411.png) , é linear e é bijectiva. Logo,
, é linear e é bijectiva. Logo,
Da mesma forma, o espaço vectorial
![]() dos polinómios de grau não superior a 2, juntamente com o polinómio nulo, é isomorfo a
dos polinómios de grau não superior a 2, juntamente com o polinómio nulo, é isomorfo a
![]() . Fixando a base de
. Fixando a base de
![]() constituída pelos polinómios
constituída pelos polinómios ![]() definidos por
definidos por
![]() e a base canónica de
e a base canónica de
![]() a transformação linear que aplica
a transformação linear que aplica ![]() em
em ![]() ,
, ![]() em
em ![]() e
e ![]() em
em ![]() é um isomorfismo de
é um isomorfismo de
![]() em
em
![]() .
.
Pelo exposto acima, é fácil agora aceitar que
Para finalizar esta secção, note que
![]() , enquanto espaço vectorial sobre
, enquanto espaço vectorial sobre
![]() , é isomorfo a
, é isomorfo a
![]() . De facto,
. De facto, ![]() e
e ![]() formam uma base de
formam uma base de
![]() , enquanto espaço vectorial sobre
, enquanto espaço vectorial sobre
![]() . São linearmente independentes (
. São linearmente independentes (![]() força
força ![]() ) e todo o complexo
) e todo o complexo ![]() escreve-se como
escreve-se como ![]() , com
, com
![]() . O isomorfismo pode ser dado pela transformação linear que aplica
. O isomorfismo pode ser dado pela transformação linear que aplica ![]() em
em ![]() e
e ![]() em
em ![]() .
.
![]()
![]()
![]()
![]()
Seguinte: Matriz associada a uma
Acima: Transformações lineares
Anterior: Definição e exemplos
Conteúdo
Pedro Patricio
2008-01-08