Matrizes diagonalizáveis

Nesta secção, vamo-nos debruçar sobre dois problemas, que aliás, e como veremos, estão relacionados. Assume-se que $A$ é uma matriz $n\times n$ sobre ${\mathbb{C}}$. Essas questões são:

# 1.

Existe uma base de ${\mathbb{C}}^n$ constituída por vectores próprios de $A$?

# 2.

Existe uma matriz $U$ invertível para a qual $U^{-1}AU$ é uma matriz diagonal?

Recordamos a noção de semelhança entre matrizes. As matriz $A$ e $B$ dizem-se semelhantes, e denota-se por $A\approx B$, se existir uma matriz invertível $U$ para a qual $B=U^{-1}AU$. Repare que as matrizes $A,B$ são necessariamente quadradas.

É óbvio que se $A\approx B$ então $B\approx A$; de facto, se $B=U^{-1}AU$ então $UBU^{-1}=A$.

Definição 5.3.1   Uma matriz quadrada $A$ diz-se diagonalizável se existir uma matriz diagonal $D$ tal que $A \approx D$. Isto é, $A=UDU^{-1}$, para alguma matriz $U$ invertível. À matriz $U$ chamamos matriz diagonalizante.

É óbvio que uma matriz diagonal é diagonalizável, bastando tomar a matriz identidade como matriz diagonalizante.

O resultado seguinte não só nos caracteriza as matrizes diagonalizáveis, mas também, à custa da sua prova, obtemos um algoritmo para encontrar a matriz diagonal e a a respectiva matriz diagonalizante.

Teorema 5.3.2   Uma matriz $n\times n$ é diagonalizável se e só se tiver $n$ vectores próprios linearmente independentes.

Em primeiro lugar, assumimos que $A$ é diagonalizável; ou seja, existe uma matriz $U=\left[\begin{array}{cccc}u_1 & u_2 &\cdots & u_n\end{array}\right]$ invertível tal que $U^{-1}AU=D=\left[\begin{array}{ccc} \lambda_1 && 0\ & \ddots &\\ 0 && \lambda_n\end{array}\right]$.

Como é óbvio, de $U^{-1}AU=D$ segue que $AU=UD$. Portanto,

$$\left[\begin{array}{cccc}Au_1 & Au_2 &\cdots & Au_n\end{array}\right] = AU=\left[\begin{array}{cccc}u_1 & u_2 &\cdots & u_n\end{array}\ri... ...gin{array}{ccc} \lambda_1 && 0\ & \ddots &\\ 0 && \lambda_n\end{array}\right]$$

$$= \left[\begin{array}{cccc}\lambda_1 u_1 & \lambda_2 u_2 &\cdots & \lambda_n u_n\end{array}\right]$$

e portanto

$$\left\{\begin{array}{ccc} Au_1&=&\lambda_1 u_1\\ Au_2&=&\lambda_2 u_2\\ \vdots & & \vdots\\ Au_n&=&\lambda_n u_n\end{array}\right. .$$

Como $U$ é invertível, então não pode ter colunas nulas, pelo que $u_i\ne 0$. Portanto, $\lambda_1,\lambda_2, \dots, \lambda_n$ são valores próprios de $A$ e $u_1,u_2,\dots,u_n$ são respectivos vectores próprios. Sendo $U$ invertível, as suas colunas são linearmente independentes, e portanto $A$ tem $n$ vectores próprios linearmente independentes.

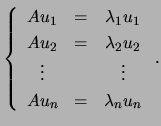
Reciprocamente, suponha que $A$ tem $n$ vectores próprios linearmente independentes. Sejam eles os vectores $u_1,u_2,\dots,u_n$, associados aos valores próprios (não necessariamente distintos) $\lambda_1,\lambda_2, \dots, \lambda_n$. Seja $U$ a matriz cujas colunas são os vectores próprios considerados acima. Ou seja, $U=\left[\begin{array}{cccc}u_1 & u_2 &\cdots & u_n\end{array}\right]$. Ora esta matriz quadrada $n\times n$ tem característica igual a $n$, pelo que é invertível. De

$$\left\{\begin{array}{ccc} Au_1&=&\lambda_1 u_1\\ Au_2&=&\lambda_2 u_2\\ \vdots & & \vdots\\ Au_n&=&\lambda_n u_n\end{array}\right.$$

segue que $\left[\begin{array}{cccc}Au_1 & Au_2 &\cdots & Au_n\end{array}\right]=\left[\b... ...y}{cccc}\lambda_1 u_1 & \lambda_2 u_2 &\cdots & \lambda_n u_n\end{array}\right]$ e portanto

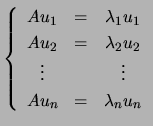
$$A\left[\begin{array}{cccc}u_1 & u_2 &\cdots & u_n\end{array}\righ... ...in{array}{ccc} \lambda_1 && 0\ & \ddots &\\ 0 && \lambda_n\end{array}\right].$$

Multiplicando ambas as equações, à esquerda, por $\left[\begin{array}{cccc}u_1 & u_2 &\cdots & u_n\end{array}\right]^{-1}$, obtemos

$$\left[\begin{array}{cccc}u_1 & u_2 &\cdots & u_n\end{array}\right... ...n{array}{ccc} \lambda_1 && 0\ & \ddots &\\ 0 && \lambda_n\end{array}\right] .$$

Realçamos o facto da demonstração do teorema nos apresentar um algoritmo de diagonalização de uma matriz $n\times n$ com $n$ vectores linearmente independentes. De facto, de $\left[\begin{array}{cccc}u_1 & u_2 &\cdots & u_n\end{array}\right]^{-1} A\left... ...gin{array}{ccc} \lambda_1 && 0\ & \ddots &\\ 0 && \lambda_n\end{array}\right]$ obtemos

$$A= \left[\begin{array}{cccc}u_1 & u_2 &\cdots & u_n\end{array}\ri... ...right] \left[\begin{array}{cccc}u_1 & u_2 &\cdots & u_n\end{array}\right]^{-1}.$$

Uma matriz diagonalizante é a matriz cujas colunas são os vectores próprios linearmente independentes dados, e a matriz diagonal correspondente é a matriz cuja entrada $(i,i)$ é o valor próprio $\lambda_i$ correspondente à coluna $i$ (e portanto ao $i-$ésimo vector próprio) da matriz diagonalizante.

Para a matriz $A=\left[\begin{array}{cc} 1&2\ 2&-2 \end{array}\right]$, vimos atrás que $\sigma(A)=\left\{-3,2\right\}$. Será $A$ diagonalizável? Um vector próprio associado ao valor próprio $-3$ é um elemento não nulo de $N(-3I_2-A)$. Encontrar um vector próprio associado a $-3$ é equivalente a encontrar uma solução não nula de $(-3I_2-A)x=0$. Fica ao cargo do leitor verificar que $\left[\begin{array}{c} -1\ 2\end{array}\right]$ é vector próprio associado ao valor próprio $-3$, e fazendo o mesmo raciocínio, que $\left[\begin{array}{c} 2\ 1\end{array}\right]$ é vector próprio associado ao valor próprio 2. Ora estes dois vectores são linearmente independentes, visto $\mathrm{car}\left[\begin{array}{cc} -1 & 2\ 2 &1\end{array}\right]=2$. Portanto, a matriz $A$ é diagonalizável, sendo a matriz diagonalizante $U=\left[\begin{array}{cc} -1 & 2\ 2 &1\end{array}\right]$ e a matriz diagonal $\left[\begin{array}{cc} -3& 0\ 0 &2 \end{array}\right]$.

Octave
A diagonalização, se possível, pode ser obtida de forma imediata como Octave:

> [q,e]=eig (A)
q =

  -0.44721  -0.89443
   0.89443  -0.44721

e =

  -3   0
   0   2

Aqui, a matriz q, ou seja, o primeiro argumento de saída de eig, indica uma matriz diagonalizante, e o segundo argumento, i.e., e, indica a matriz diagonal cujas entradas diagonais são os valores próprios. Repare, ainda, que a coluna $i$ de q é um vector próprio associado ao valor próprio que está na entrada $(i,i)$ de e. Façamos, então, a verificação:

> q*e*inverse (q)
ans =

   1.0000   2.0000
   2.0000  -2.0000

Considere agora a matriz $B=\left[\begin{array}{cc} 0&0\ 1&0\end{array}\right]$. Esta matriz é nilpotente, pelo que $\sigma(B)=\left\{0\right\}$. O espaço próprio associado a 0 é $N(-B)=N(B)$. Ora $\mathrm{car}(B)=1$, pelo que $\mathrm{nul}(B)=1$, e portanto a multiplicidade geométrica do valor próprio 0 é 1 (repare que a multiplicidade algébrica do valor próprio 0 é 2). Ou seja, não é possível encontrar 2 vectores próprios linearmente independentes.

Octave
Considere a matriz C=[2 1; 0 2]. Sendo triangular superior, os seus valores próprios são os elementos diagonais da matriz. Isto é, $\sigma(C)=\left\{2\right\}$. Repare que a multiplicidade algébrica do valor próprio $2$ é 2.

> eig (C)
ans =

  2
  2

Repare que $\mathrm{car}(2*I_2-C)=\mathrm{car}\left[\begin{array}{cc} 0& 1\ 0&0\end{array}\right]=1$, pelo que $\mathrm{nul}(2*I_2-C) =1$. Logo, não é possível encontrar 2 vectores próprios de $C$ linearmente independentes, e portanto $C$ não é diagonalizável.

> rank(2*eye(2)-C)
ans = 1
> [q,e]=eig (C)
q =

    1  NaN
    0  NaN

e =

  2  0
  0  2

É, todavia, apresentada uma base do espaço próprio de $C$ associado ao valor próprio 2, nomeadamente a primeira coluna da matriz q.

Considere agora a matriz $A=\left[\begin{array}{ccc} 1& 2& 1\ 2 &-2& 2\ 0& 0& -3\end{array}\right]$. Octave
Para A=[1 2 1;2 -2 2; 0 0 -3] tem-se $\sigma(A)=\left\{-3,2\right\}$, sendo as multiplicidades algébricas de $-3$ e $2$, respectivamente, 2 e 1.

> eig (A)
ans =

   2
  -3
  -3

Como $\mathrm{car}(-3I_3-A)=2$, temos que $\mathrm{nul}(-3I_3-A)=1$, e portanto a multiplicidade geométrica do valor próprio $-3$ é 1. Portanto, a matriz não é diagonalizável pois não é possível encontrar 3 vectores próprios linearmente independentes.

> [q,e]=eig (A)
q =

   0.89443  -0.44721       NaN
   0.44721   0.89443       NaN
   0.00000   0.00000       NaN

e =

   2   0   0
   0  -3   0
   0   0  -3

A primeira coluna de q é um vector próprio associado a 2 e a segunda coluna de q é um vector próprio associado a $-3$

O que se pode dizer em relação à independência linear de um vector próprio associado a $-3$ e um vector próprio associado a $2$?

Teorema 5.3.3   Sejam $v_1,v_2,\dots,v_k$ vectores próprios associados a valores próprios $\lambda_1,\lambda_2,\dots,\lambda_k$ distintos entre si. Então $\left\{v_1,v_2,\dots,v_k\right\}$ é um conjunto linearmente independente.

Suponhamos que $\left\{v_1,v_2,\dots,v_k\right\}$ é um conjunto linearmente dependente, sendo $v_1,v_2,\dots,v_k$ vectores próprios associados a valores próprios $\lambda_1,\lambda_2,\dots,\lambda_k$ distintos entre si. Pretendemos, desta forma, concluir um absurdo.

Seja $r$ o menor inteiro para o qual o conjunto $\left\{v_1,v_2, \dots, v_r \right\}$ é linearmente independente. Ora $r\ge 1$ já que $v_1\ne 0$ (pois é $v_1$ é vector próprio) e $r< k$ já que o conjunto dos vectores próprios é linearmente dependente. Sendo o conjunto $\left\{v_1,v_2,\dots,v_{r+1}\right\}$ linearmente dependente, existem escalares $\alpha_1,\alpha_2,\dots,\alpha_r,\alpha_{r+1}$ não todos nulos para os quais

$$\sum_{i=1}^{r+1}\alpha_iv_i=0$$

o que implica que $A\sum_{i=1}^{r+1}\alpha_iv_i =\sum_{i=1}^{r+1}\alpha_iAv_i=0$, e portanto

$$\sum_{i=1}^{r+1}\alpha_i\lambda_i v_i=0.$$

Por outro lado, $\sum_{i=1}^{r+1}\alpha_iv_i=0$ implica que $\lambda_{r+1}\sum_{i=1}^{r+1}\alpha_iv_i=0$ e portanto

$$\sum_{i=1}^{r+1}\alpha_i\lambda_{r+1} v_i=0.$$

Fazendo a diferença das duas equações, obtemos $\sum_{i=1}^{r+1}\alpha_i(\lambda_i-\lambda_{r+1})v_i=0$, e portanto $\sum_{i=1}^{r}\alpha_i(\lambda_i-\lambda_{r+1})v_i=0$. Como $\left\{v_1,v_2, \dots, v_r \right\}$ é linearmente independente, segue que $\alpha_i(\lambda_i-\lambda_{r+1})=0$, o que implica, e visto $\lambda_i-\lambda_{r+1}\ne 0$ já que os valores próprios são distintos, que $\alpha_i=0$, com $i=1 \dots, r$. Mas $\sum_{i=1}^{r+1}\alpha_iv_i=0$, o que juntamente com as igualdades $\alpha_i=0$, com $i=1 \dots, r$, leva a que $\alpha_{r+1} v_{r+1}=0$. Como $v_{r+1}\ne 0$ já que é vector próprio, segue que $\alpha_{r+1}=0$. Tal contradiz o facto de existirem escalares $\alpha_1,\alpha_2,\dots,\alpha_r,\alpha_{r+1}$ não todos nulos para os quais $\sum_{i=1}^{r+1}\alpha_iv_i=0$.

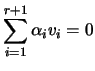
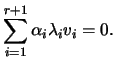
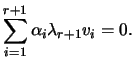
Alertamos para o facto do recíproco do teorema ser falso. Repare que a matriz identidade $I_n$ tem $1$ como único valor próprio, e a dimensão de $N(I_n -I_n)$ ser $n$, e portanto há $n$ vectores próprios linearmente independentes associados a $1$.

Se uma matriz $n\times n$ tem os seus $n$ valores próprios distintos então, pelo teorema, tem $n$ vectores próprios linearmente independentes, o que é equivalente a afirmar que a matriz é diagonalizável.

Corolário 5.3.4   Uma matriz com os seus valores próprios distintos é diagonalizável.

Mais uma vez alertamos para o facto do recíproco do corolário ser falso. Isto é, há matrizes diagonalizáveis que têm valores próprios com multiplicidade algébrica superior a 1. Octave
Considere a matriz A=[0 0 -2; 1 2 1; 1 0 3]. Esta matriz tem dois valores próprios distintos.

> A=[0 0 -2; 1 2 1; 1 0 3];
> eig(A)
ans =

  2
  1
  2

Repare que o valor próprio 2 tem multiplicidade algébrica igual a 2, enquanto que a multiplicidade algébrica do valor próprio 1 é 1. Pelo teorema anterior, um vector próprio associado a 2 e um vector próprio associado a 1 são linearmente independentes. Repare que a multiplicidade geométrica de $2$ é também 2, calculando rank(2*eye(3)-A).

> rank(2*eye(3)-A)
ans = 1

Como a característica de $2I_3-A$ é 1 então $\mathrm{nul}(2I_3-A)=2$, e portanto existem dois vectores próprios linearmente independentes associados a $2$. Uma base do espaço próprio associado a 2 pode ser obtida assim:

> null(2*eye(3)-A)
ans =

  -0.70711   0.00000
   0.00000   1.00000
   0.70711   0.00000

Estes juntamente com um vector próprio associado ao valor próprio 1 formam um conjunto linearmente independente, pois vectores próprios associados a valor próprios distintos são linearmente independentes. Ou seja, há 3 vectores próprios linearmente independentes, donde segue que a matriz $A$ é diagonalizável.

> [v,e]=eig (A)
v =

   0.00000  -0.81650   0.70656
   1.00000   0.40825   0.03950
   0.00000   0.40825  -0.70656

e =

  2  0  0
  0  1  0
  0  0  2

> v*e*inverse(v)
ans =

  -0.00000   0.00000  -2.00000
   1.00000   2.00000   1.00000
   1.00000   0.00000   3.00000