



Seguinte: Matrizes diagonalizáveis
Acima: Valores e vectores próprios
Anterior: Motivação e definições
Conteúdo
Nos resultados que se seguem descrevemos algumas propriedades dos valores própios.
Teorema 5.2.1
Dada uma matriz quadrada
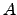
,
Recorde que
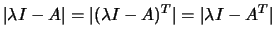 .
.
Teorema 5.2.2
Os valores próprios de uma matriz triangular (inferior ou superior) são os seus elementos diagonais.
Seja
![$ A=[a_{ij}]$](img238.png) triangular superior,
triangular superior,
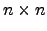 . Ora
. Ora 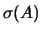 é o conjunto das soluções de
é o conjunto das soluções de
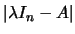 . Mas
. Mas
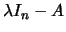 é de novo uma matriz triangular superior já que
é de novo uma matriz triangular superior já que
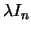 é diagonal. Portanto
é diagonal. Portanto
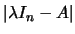 é o produto dos seus elementos diagonais, ou seja,
é o produto dos seus elementos diagonais, ou seja,
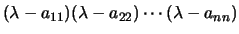 , que tem como raizes
, que tem como raizes
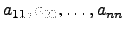 .
.
Teorema 5.2.3
Uma matriz
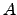
, quadrada, é invertível se e só se
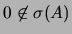
.
Sejam 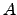 uma matriz quadrada de ordem
uma matriz quadrada de ordem 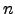 e
e
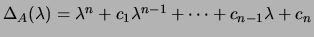 o polinómio característico de
o polinómio característico de 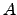 . Ora
. Ora
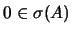 se e só
se 0 é raiz de
se e só
se 0 é raiz de 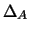 , ou de forma equivalente,
, ou de forma equivalente, 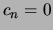 .
.
Por definição,
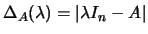 . Tomando
. Tomando 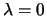 obtemos
obtemos
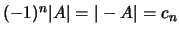 . tal implica que
. tal implica que 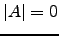 se e só se
se e só se
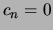 . Portanto
. Portanto 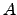 não é invertível se e só se
não é invertível se e só se 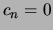 o que por
sua vez vimos ser equivalente a
o que por
sua vez vimos ser equivalente a
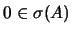 .
.
Teorema 5.2.4
Sejam
uma matriz quadrada e
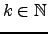
. Se
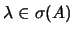
e
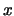
é
vector próprio associado a
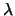
então
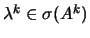
e
é vector próprio de
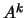
associado a
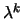
.
Se
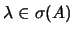 e
e 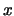 é vector próprio associado a
é vector próprio associado a
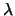 então
então
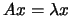 . Desta igualdade segue que, para
qualquer
. Desta igualdade segue que, para
qualquer
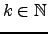 , se tem
e portanto
, se tem
e portanto
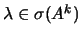 e
e 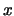 é vector próprio de
é vector próprio de 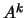 associado a
associado a 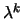 .
.
Recordamos que uma matriz 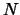 ,
, 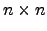 , se diz nilpotente se existir um natural
, se diz nilpotente se existir um natural
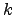 para o qual
para o qual
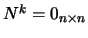 .
.
Alertamos ainda para o facto de
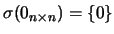 ;
isto é, a matriz nula só tem um valor próprio: o zero.
;
isto é, a matriz nula só tem um valor próprio: o zero.
Corolário 5.2.5
Se
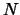
é uma matriz nilpotente então
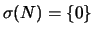
.
Suponha que 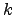 é tal que
é tal que
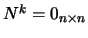 . Seja
. Seja
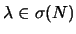 . Então
. Então 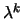 é valor próprio de
é valor próprio de
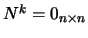 ;
portanto,
;
portanto,
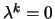 , do que segue que
, do que segue que 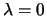 .
.
Terminamos esta secção com duas observações, omitindo a sua prova:
- (i)
- O determinante de uma matriz iguala o produto dos seus valores próprios.
- (ii)
- O traço de uma matriz (ou seja, a soma dos elementos diagonais de uma matriz) iguala a soma dos seus valores próprios.




Seguinte: Matrizes diagonalizáveis
Acima: Valores e vectores próprios
Anterior: Motivação e definições
Conteúdo
Pedro Patricio
2008-01-08
![]() . Tomando
. Tomando ![]() obtemos
obtemos
![]() . tal implica que
. tal implica que ![]() se e só se
se e só se
![]() . Portanto
. Portanto ![]() não é invertível se e só se
não é invertível se e só se ![]() o que por
sua vez vimos ser equivalente a
o que por
sua vez vimos ser equivalente a
![]() .
.
![]() ,
, ![]() , se diz nilpotente se existir um natural
, se diz nilpotente se existir um natural
![]() para o qual
para o qual
![]() .
.
![]() ;
isto é, a matriz nula só tem um valor próprio: o zero.
;
isto é, a matriz nula só tem um valor próprio: o zero.
![]()
![]()
![]()
![]()