



Seguinte: Regra de Cramer
Acima: Sistemas de equações lineares
Anterior: Resolução de
Conteúdo
A aplicação do Algoritmo de Eliminação de Gauss na resolução de um sistema de equações lineares reduz o problema inicial a um outro, equivalente ao dado (ou seja, com o mesmo conjunto de soluções) onde a matriz associada ao sistema é escada de linhas. Tal permite a utilização do algoritmo da susbstituição inversa por forma a se encontrar (caso existam) as soluções para o problema. Nesse método, o valor das incógnitas básicas era encontrado à custa das incógnitas livres e dos termos independentes, bem como do valor das incógnitas básicas encontrado no passo anterior, no sentido sul
 norte do vector das incógnitas. Recorde que no AEG a estratégia tinha como objectivo, por operações elementares de linhas, obter zeros por debaixo de cada pivot, estratégia essa implementada no sentido NW
norte do vector das incógnitas. Recorde que no AEG a estratégia tinha como objectivo, por operações elementares de linhas, obter zeros por debaixo de cada pivot, estratégia essa implementada no sentido NW
 SE. Este raciocínio pode ser estendido a obterem-se zeros por cima dos pivots, no sentido SW
SE. Este raciocínio pode ser estendido a obterem-se zeros por cima dos pivots, no sentido SW
 NE, por operações elementares de linhas. De facto, neste processo estão ausentes trocas de linhas, já que os pivots usados neste novo processo são que estiveram envolvidos na fase inicial correspondente ao AEG. O resultado final será uma matriz constituída pelos pivots, tendo estes zeros por debaixo e por cima. Ou seja, se se dividir cada linha não nula pelo pivot respectivo, obtemos uma matriz da forma, a menos de trocas de colunas, uma matriz da forma
NE, por operações elementares de linhas. De facto, neste processo estão ausentes trocas de linhas, já que os pivots usados neste novo processo são que estiveram envolvidos na fase inicial correspondente ao AEG. O resultado final será uma matriz constituída pelos pivots, tendo estes zeros por debaixo e por cima. Ou seja, se se dividir cada linha não nula pelo pivot respectivo, obtemos uma matriz da forma, a menos de trocas de colunas, uma matriz da forma
![$ \left[\begin{array}{c\vert c}
I_k & M \hline
0 & 0\end{array}\right]$](img709.png) , podendo os blocos nulos não existir. A este método (à excepção da possível troca de colunas) é denominado o algoritmo de Gauss-Jordan, e a matriz obtida diz-se que está na forma canónica (reduzida) de linhas, ou na forma normal (ou canónica) de Hermite. Ou seja, a matriz
, podendo os blocos nulos não existir. A este método (à excepção da possível troca de colunas) é denominado o algoritmo de Gauss-Jordan, e a matriz obtida diz-se que está na forma canónica (reduzida) de linhas, ou na forma normal (ou canónica) de Hermite. Ou seja, a matriz
![$ H=[h_{ij}]$](img710.png) ,
, 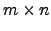 , obtida satisfaz:
, obtida satisfaz:
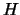 é triangular superior,
é triangular superior,
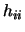 é ou 0 ou 1,
é ou 0 ou 1,
- se
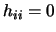 então
então 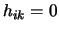 , para cada
, para cada 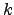 tal que
tal que
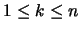 ,
,
- se
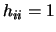 então
então 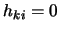 para cada
para cada 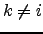 .
.
Repare que só são realizadas operações elementares nas linhas da matriz. A aplicação deste método na resolução de uma sistema de equações lineares permite obter, de forma imediata, o valor das incógnitas básicas. Apesar deste método parecer mais atractivo que o de Gauss (ou suas variantes), em geral é menos eficiente do ponto de vista computacional.
Octave
![\includegraphics[scale=0.3]{Octave_Sombrero.eps}](img64.png)
Considere a matriz
![$ A=\left[\begin{array}{cccc} 1 & 2 & 3 & 3\\
2 & 0 & 1 & -1\\
0 & 0 &-1 & -3\end{array}\right]$](img718.png) . A forma normal de Hermite de
. A forma normal de Hermite de 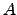 é
é
> rref (A)
ans =
1 0 0 -2
0 1 0 -2
0 0 1 3
Ora se 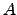 for a matriz aumentada associada a um sistema de equações lineares, a forma canónica apresentada atrás fornece-nos uma solução para o sistema, no caso
for a matriz aumentada associada a um sistema de equações lineares, a forma canónica apresentada atrás fornece-nos uma solução para o sistema, no caso 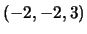 .
.
No que se segue, mostramos como se aplica o algoritmo de Gauss-Jordan para inverter matrizes.
Seja 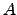 uma matriz
uma matriz 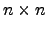 , não-singular. Ou seja, invertível. De forma equivalente, existe uma única matriz
, não-singular. Ou seja, invertível. De forma equivalente, existe uma única matriz 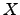 tal que
tal que 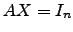 . Denotemos a matriz
. Denotemos a matriz 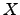 , que pretendemos obter, à custa das suas colunas:
, que pretendemos obter, à custa das suas colunas:
![$ X=\left[\begin{array}{cccc} X_1 & X_2 &\cdots &X_n \end{array}\right]$](img720.png) . Pela forma como está definido o produto matricial, e tomando
. Pela forma como está definido o produto matricial, e tomando 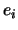 como a
como a 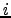 -ésima coluna da matriz
-ésima coluna da matriz 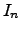 , a igualdade
, a igualdade 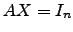 pode-se escrever como
pode-se escrever como
![$ \left[\begin{array}{cccc} AX_1 & AX_2 &\cdots &AX_n \end{array}\right]=\left[\begin{array}{cccc} e_1 & e_2 & \cdots &e_n\end{array}\right]$](img722.png) . Surgem-nos, então,
. Surgem-nos, então, 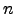 equações matriciais:
equações matriciais:
Como 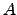 é invertível, cada uma destas equações é consistente e tem apenas uma solução. A solução de
é invertível, cada uma destas equações é consistente e tem apenas uma solução. A solução de 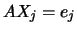 é a coluna
é a coluna 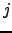 da matriz
da matriz 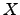 inversa de
inversa de 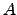 que pretendemos calcular. Poder-se-ia aplicar a estratégia de Gauss a cada uma destas equações, ou seja, à matriz aumentada
que pretendemos calcular. Poder-se-ia aplicar a estratégia de Gauss a cada uma destas equações, ou seja, à matriz aumentada
![$ \left[\begin{array}{c\vert c}A &e_j \end{array}\right]$](img725.png) . Como a matriz do sistema é a mesma, as operações elementares envolvidas seriam as mesmas para as
. Como a matriz do sistema é a mesma, as operações elementares envolvidas seriam as mesmas para as 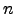 equações. Essas operações elementares podem ser efectuadas simultaneamente, considerando a matriz aumentada
equações. Essas operações elementares podem ser efectuadas simultaneamente, considerando a matriz aumentada
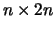 Sendo a matriz invertível, a matriz escada de linhas
Sendo a matriz invertível, a matriz escada de linhas 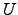 obtida de
obtida de 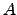 por aplicação do AEG tem elementos diagonais não nulos, que são os pivots que surgem na implementação do algoritmo. Aplicando Gauss-Jordan (ou seja, no sentido SE
por aplicação do AEG tem elementos diagonais não nulos, que são os pivots que surgem na implementação do algoritmo. Aplicando Gauss-Jordan (ou seja, no sentido SE
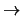 NW, criando zeros por cima dos pivots que se vão considerando), obtemos uma matriz da forma
NW, criando zeros por cima dos pivots que se vão considerando), obtemos uma matriz da forma
![\begin{displaymath}\left[\begin{array}{c\vert c}
\begin{array}{cccc} d_1 & 0& \d...
...ay}{cccc}
Y_1 & Y_2 & \cdots & Y_n\end{array}\end{array}\right]\end{displaymath}](img728.png) . Dividindo a linha
. Dividindo a linha 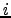 por
por 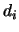 , para
, para 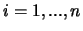 , obtém-se a matriz
Ora tal significa que
, obtém-se a matriz
Ora tal significa que
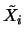 é a solução de
é a solução de 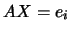 . Ou seja, o segundo bloco da matriz aumentada indicada atrás não é mais que a inversa da matriz
. Ou seja, o segundo bloco da matriz aumentada indicada atrás não é mais que a inversa da matriz  . Isto é, Gauss-Jordan forneceu a matriz
. Isto é, Gauss-Jordan forneceu a matriz
![$ \left[\begin{array}{c\vert c} I_n & A^{-1}\end{array}\right]$](img734.png) .
.




Seguinte: Regra de Cramer
Acima: Sistemas de equações lineares
Anterior: Resolução de
Conteúdo
Pedro Patricio
2008-01-08
![$ \left[\begin{array}{c\vert c}
I_k & M \hline
0 & 0\end{array}\right]$](img709.png) , podendo os blocos nulos não existir. A este método (à excepção da possível troca de colunas) é denominado o algoritmo de Gauss-Jordan, e a matriz obtida diz-se que está na forma canónica (reduzida) de linhas, ou na forma normal (ou canónica) de Hermite. Ou seja, a matriz
, podendo os blocos nulos não existir. A este método (à excepção da possível troca de colunas) é denominado o algoritmo de Gauss-Jordan, e a matriz obtida diz-se que está na forma canónica (reduzida) de linhas, ou na forma normal (ou canónica) de Hermite. Ou seja, a matriz
![\includegraphics[scale=0.3]{Octave_Sombrero.eps}](img64.png)
![$ A=\left[\begin{array}{cccc} 1 & 2 & 3 & 3\\
2 & 0 & 1 & -1\\
0 & 0 &-1 & -3\end{array}\right]$](img718.png) . A forma normal de Hermite de
. A forma normal de Hermite de ![$\displaystyle \left[\begin{array}{c\vert c}
A& \begin{array}{cccc}
1 & 0 & \cdo...
... 1 & &\vdots \\
& \cdots &&\\
0 & \cdots & 0 &1\end{array}\end{array}\right].$](img727.png)
![\begin{displaymath}\left[\begin{array}{c\vert c}
\begin{array}{cccc} d_1 & 0& \d...
...ay}{cccc}
Y_1 & Y_2 & \cdots & Y_n\end{array}\end{array}\right]\end{displaymath}](img728.png) . Dividindo a linha
. Dividindo a linha