Dada uma matriz ![]() , quadrada de ordem
, quadrada de ordem ![]() , denota-se por
, denota-se por ![]() a submatriz de
a submatriz de ![]() obtida por remoção da sua linha
obtida por remoção da sua linha ![]() e da sua coluna
e da sua coluna ![]() .
.
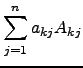 |
|||
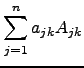 |
O teorema anterior é o caso especial de um outro que enunciaremos de seguida. Para tal, é necessário introduzir mais notação e algumas definições (cf. [10]).
Seja ![]() uma matriz
uma matriz ![]() . Um menor de ordem
. Um menor de ordem ![]() de
de ![]() , com
, com
![]() , é o determinante de uma submatriz
, é o determinante de uma submatriz ![]() de
de ![]() , obtida de
, obtida de ![]() eliminando
eliminando ![]() linhas e
linhas e ![]() colunas de
colunas de ![]() .
.
Considere duas sequências crescentes de números
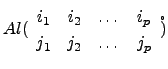 . Ou seja,
. Ou seja,
![$\displaystyle A\l (\begin{array}{cccc} i_1& i_2& \dots &i_p j_1&j_2& \dots &j_p\end{array}\r) = \vert\left[a_{i_k j_k}\right]_{k=1,\dots p} \vert.$](img594.png)
Paralelamente, podemos definir os menores complementares de ![]() como os determinantes das submatrizes a que se retiraram linhas e colunas. Se
como os determinantes das submatrizes a que se retiraram linhas e colunas. Se ![]() for
for
![]() ,
,
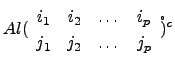
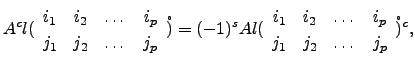
O caso em que ![]() coincide com o exposto no início desta secção.
coincide com o exposto no início desta secção.
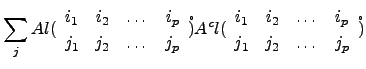 |
Para finalizar, apresentamos um método de cálculo da inversa de uma matriz não singular.
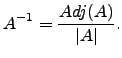
Octave
![\includegraphics[scale=0.3]{Octave_Sombrero.eps}](img64.png)
Vamos agora apresentar uma pequena função que tem como entrada uma matriz quadrada e como saída sua matriz adjunta.
function ADJ=adjunta(A)
% sintaxe: adjunta(A)
% onde A e' uma matriz quadrada
% use-a por sua propria conta e risco
% copyleft ;-) Pedro Patricio
n=size(A)(1,1); % n e' o numero de linhas da matriz
ADJ= zeros (n); % inicializacao da matriz ADJ
for i=1:n % i denota a linha
for j=1:n % j denota a coluna
submatriz=A([1:i-1 i+1:n],[1:j-1 j+1:n]); % submatriz e' a
submatriz de A a que se lhe retirou a linha i e a coluna j
cofactor=(-1)^(i+j)* det(submatriz); % calculo do cofactor
ADJ(j,i)=cofactor; % ADJ é a transposta da matriz dos
cofactores; repare que a entrada (j,i) e' o cofactor (i,j) de A
end; % fim do ciclo for em j
end % fim do ciclo for em i
Grave a função, usando um editor de texto, na directoria de leitura do Octave. No Octave, vamos criar uma matriz ![]() :
:
> B=fix(10*rand(4,4)-5)
B =
0 -2 3 -2
-2 3 1 -1
-3 0 4 3
-4 4 0 4
> adjunta(B)
ans =
76.0000 -36.0000 -48.0000 65.0000
48.0000 -32.0000 -28.0000 37.0000
36.0000 -24.0000 -32.0000 36.0000
28.0000 -4.0000 -20.0000 17.0000
Pelo teorema, como
![]() segue que
segue que
![]() .
.
> B*adjunta(B)
ans =
-44.00000 -0.00000 0.00000 0.00000
0.00000 -44.00000 -0.00000 0.00000
0.00000 -0.00000 -44.00000 0.00000
0.00000 -0.00000 0.00000 -44.00000
![]()
![]()
![]()
![]()
Seguinte: Sistemas de equações lineares
Acima: Determinantes
Anterior: Propriedades
Conteúdo
Pedro Patricio
2008-01-08