Seja ![]() uma matriz
uma matriz ![]() não nula.
não nula.
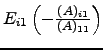 .
.
Após se aplicar o passo 3 em todas as linhas e na primeira coluna, e supondo que
![]() , a matriz que se obtem tem a forma seguinte:
, a matriz que se obtem tem a forma seguinte:
![$\displaystyle \left[\begin{array}{cccc}
(A)_{11} &(A)_{12} &(A)_{13} &(A)_{1n} ...
... & ?\\
0 & ? & ? & ?\\
\vdots & ? & ? & ?\\
0 & ? & ? & ?\end{array}\right].$](img367.png)
![$ \left[\begin{array}{c\vert c}
(A)_{11}& * \hline
0 & \widetilde A\end{array}\right]$](img368.png) . O algoritmo continua agora aplicado à matriz
. O algoritmo continua agora aplicado à matriz
![$ \left[\begin{array}{c\vert c}
(A)_{11}& * \hline
0 & \widetilde A\end{array}\right]$](img368.png) . As operações elementares efectuadas em
. As operações elementares efectuadas em
![$ \left[\begin{array}{c\vert c}
(\widetilde A)_{11}& * \hline
0 & \widetilde{\widetilde A}\end{array}\right]$](img369.png) , onde assumimos
, onde assumimos
![$ \left[\begin{array}{c\vert c}
(A)_{11}& * \hline
0 & \widetilde A\end{array}\right]$](img368.png) dão lugar à matriz
dão lugar à matriz
![$ \left[\begin{array}{cc\vert c}
(A)_{11}& \dots &(A)_{1m}\\
0 & (\widetilde A)_{11}& * \hline
0 & 0 & \widetilde{\widetilde A}\end{array}\right]$](img371.png) . Note que se assumiu que as entradas
. Note que se assumiu que as entradas ![$ M=\left[\begin{array}{cccc}
2 & 2 & 2 & 2\\
2 & 2 & 2 & 0\\
1 & 1 & 0 & 1\end{array}\right]$](img373.png) . Multiplicando esta matriz, à esquerda, por
. Multiplicando esta matriz, à esquerda, por
![$ M_2=\left[\begin{array}{c\vert ccc}
2 & 2 & 2 & 2 \hline
0 & 0 & 0 &-2\\
0 & 0 &-1 & 0\end{array}\right]$](img375.png) . Aplicamos agora o algoritmo à submatriz
. Aplicamos agora o algoritmo à submatriz
![$ \widetilde M=\left[\begin{array}{ccc}
0 & 0 &-2\\
0 &-1 & 0\end{array}\right]$](img376.png) . Note que a esta submatriz teremos que aplicar (2) por impossibilidade de se usar (1); de facto, não há elementos não nulos na primeira coluna de
. Note que a esta submatriz teremos que aplicar (2) por impossibilidade de se usar (1); de facto, não há elementos não nulos na primeira coluna de
![$ \widetilde M_2=\left[\begin{array}{cc} 0 &-2\\
-1 & 0\end{array}\right]$](img379.png) . É necessário fazer a troca das linhas por forma a obtermos um elemento não nulo que terá as funções de pivot. Essa troca de linhas é uma operação elementar também na matriz original
. É necessário fazer a troca das linhas por forma a obtermos um elemento não nulo que terá as funções de pivot. Essa troca de linhas é uma operação elementar também na matriz original
![$ M_2=\left[\begin{array}{cc\vert cc}
2 & 2 & 2 & 2 \hline
0 & 0 & 0 &-2\\
0 & 0 &-1 & 0\end{array}\right]$](img380.png) . Tal corresponde a multiplicá-la, à esquerda, por
. Tal corresponde a multiplicá-la, à esquerda, por ![$ \left[\begin{array}{cccc}
2 & 2 & 2 & 2\\
0 & 0 & -1 & 0\\
0 & 0 & 0 & 2\end{array}\right]$](img382.png) . A matriz obtida tem uma particularidade: debaixo de cada pivot todos os elementos são nulos.
. A matriz obtida tem uma particularidade: debaixo de cada pivot todos os elementos são nulos.
Octave
![\includegraphics[scale=0.3]{Octave_Sombrero.eps}](img64.png)
I3 indica a matriz identidade de ordem 3.
> M=[2 2 2 2;2 2 2 0;1 1 0 1] > P23=I3([1 3 2],:); > E31=I3; E31(3,1)=-0.5; > E21=I3; E21(2,1)=-1; > P23*E31*E21*M U = 2 2 2 2 0 0 -1 0 0 0 0 -2
Como foi referido, a matriz obtida por aplicação dos passos descritos no Algoritmo de Eliminação de Gauss tem uma forma muito particular. De facto, debaixo de cada pivot todos os elementos são nulos. A esse tipo de matriz chamamos matriz escada (de linhas). Uma matriz
![]() é matriz escada (de linhas) se
é matriz escada (de linhas) se
Sempre que o contexto o permita, diremos matriz escada para significar matriz escada de linhas.
A matriz
![$ U=\left[\begin{array}{cccc}
2 & 2 & 2 & 2\\
0 & 0 & -1 & 0\\
0 & 0 & 0 & 2\end{array}\right]$](img389.png) é uma matriz escada (de linhas) que se obteve de
é uma matriz escada (de linhas) que se obteve de ![]() por aplicação dos passos
por aplicação dos passos ![]() -
-![]() . É óbvio que uma matriz escada é triangular superior, mas o recíproco não é válido em geral. Como exemplo, considere a matriz
. É óbvio que uma matriz escada é triangular superior, mas o recíproco não é válido em geral. Como exemplo, considere a matriz
![$ \left[\begin{array}{cc} 0 & 1 0 &1\end{array}\right]$](img391.png) .
.
Ou seja, a matriz ![]() iguala
iguala ![]() . Portanto, toda a matriz é equivalente por linhas a uma matriz escada de linhas.
. Portanto, toda a matriz é equivalente por linhas a uma matriz escada de linhas.
Antes de procedermos à prova deste resultado, abrimos um parênteses para apresentarmos dois exemplos que servem de motivação ao lema que se segue.
Considere a matriz
![$ A=\left[\begin{array}{ccc} 0 & 3 & -2\\
-1 & 3 & 0\\
1 & 3 & -5\end{array}\right]$](img394.png) . A troca da primeira com a segunda linhas dá origem à matriz
. A troca da primeira com a segunda linhas dá origem à matriz
![$ \widetilde A= \left[\begin{array}{ccc}
-1 & 3 & 0\\
0 & 3 & -2\\
1 & 3 & -5\end{array}\right]$](img395.png) , a qual, e usando o AEG descrito atrás, satisfaz
, a qual, e usando o AEG descrito atrás, satisfaz
![$ E_{32}(-3) E_{31}(2) \widetilde A = \left[\begin{array}{ccc}
-1 & 3 & 0\\
0 & 3 &-2\\
0 & 0 & 1\end{array}\right]$](img396.png) . Ou seja, existem matrizes
. Ou seja, existem matrizes ![]() permutação,
permutação, ![]() triangular inferior com 1's na diagonal e
triangular inferior com 1's na diagonal e ![]() matriz escada para as quais
matriz escada para as quais ![]() . Para tal, basta tomar
. Para tal, basta tomar
![\begin{displaymath}P=\left[
\begin{array}{ccc}
0 & 1 & 0\\
1 & 0 & 0\\
0 & 0 & 1\end{array}\right]\end{displaymath}](img397.png) ,
,
![]() , e
, e
![$ U=\left[\begin{array}{ccc}
-1 & 3 & 0\\
0 & 3 &-2\\
0 & 0 & 1\end{array}\right]$](img399.png) .
.
Considere agora a matriz
![$ M=\left[\begin{array}{ccc}
1 & 1 & 1\\
0 & 0 & 1\\
1 & 0 & 1\end{array}\right]$](img400.png) . Ora
. Ora
![$ E_{31}(-1) M=\left[\begin{array}{ccc} 1& 1 & 1\\
0 & 0 & 1\\
0 & -1 & 0\end{array}\right]$](img401.png) , o que força a troca da segunda pela terceira linha. Obtemos, assim,
, o que força a troca da segunda pela terceira linha. Obtemos, assim,
![$ P_{23} E_{31}(-1) M=\left[\begin{array}{ccc} 1& 1 & 1\\
0 & -1 & 0\\
0 & 0 & 1\end{array}\right]$](img402.png) , que é uma matriz escada. Neste caso, como se obtêm as matrizes
, que é uma matriz escada. Neste caso, como se obtêm as matrizes ![]() do teorema? Ao contrário do exemplo anterior, a realização matricial das operações elementares por linhas do AEG não nos fornece, de forma imediata, essa factorização. No entanto, poder-se-ia escrever
do teorema? Ao contrário do exemplo anterior, a realização matricial das operações elementares por linhas do AEG não nos fornece, de forma imediata, essa factorização. No entanto, poder-se-ia escrever
![$ E_{31}(-1) M = P_{23}
\left[\begin{array}{ccc} 1& 1 & 1\\
0 & -1 & 0\\
0 & 0 & 1 \end{array}\right]$](img404.png) , já que
, já que
![]() , e portanto
, e portanto
![$ M=E_{31}(1) P_{23} \left[\begin{array}{ccc} 1& 1 & 1\\
0 & -1 & 0\\
0 & 0 & 1\end{array}\right]$](img406.png) , pois
, pois
![]() . Note que
. Note que
![]() . Não obstante, repare que
. Não obstante, repare que
![]() , donde
, donde
![$ M=P_{23} E_{21}(1) \left[\begin{array}{ccc} 1& 1 & 1\\
0 & -1 & 0\\
0 & 0 & 1\end{array}\right]$](img410.png) , e portanto
, e portanto ![]() , com
, com
![]() e
e
![$ U=\left[\begin{array}{ccc} 1& 1 & 1\\
0 & -1 & 0\\
0 & 0 & 1\end{array}\right]$](img412.png) .
.
Suponha que ![]() . Pretende-se mostrar que
. Pretende-se mostrar que
![]() , com
, com ![]() .
Sendo
.
Sendo
![]() a matriz obtida de
a matriz obtida de ![]() trocando as linhas
trocando as linhas ![]() e
e ![]() , e visto a linha
, e visto a linha ![]() de
de ![]() ser
ser

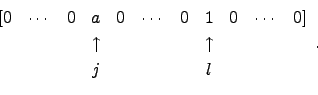
![]() é a matriz obtida de
é a matriz obtida de ![]() a que à linha
a que à linha ![]() se somou a linha
se somou a linha ![]() de
de ![]() multiplicada por
multiplicada por ![]() . Sendo a linha
. Sendo a linha ![]() de
de ![]()
![\begin{displaymath}\begin{array}{ccccccccc}
[ 0 & \cdots & 0 & \cdots &0 & 1 & ...
...ts &0 ] \\
& & & && \uparrow &\\
& & & & & l & &\end{array}\end{displaymath}](img428.png)
![\begin{displaymath}\begin{array}{ccccccccc}
[ 0 & \cdots & 0 & \cdots &0 & 1 & ...
...ts &0 ] \\
& & & && \uparrow &\\
& & & & & j & &\end{array}\end{displaymath}](img430.png)
![\begin{displaymath}\begin{array}{ccccccccc}
[ 0 & \cdots & 0 & \cdots &0 & 1 & 0...
...dots &0 ] \\
& & & && \uparrow &\\
& & & & & j & &\end{array}\end{displaymath}](img431.png) |
|||
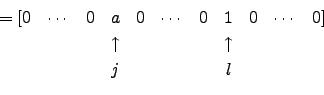 |
Para ![]() , a linha
, a linha ![]() de
de
![]() é a linha
é a linha ![]() de
de ![]() , sendo esta a linha
, sendo esta a linha ![]() da matriz identidade se
da matriz identidade se ![]() , ou a linha
, ou a linha ![]() da identidade se
da identidade se ![]() . Por sua vez, a linha
. Por sua vez, a linha ![]() de
de
![]() é a linha
é a linha ![]() da ientidade se
da ientidade se ![]() , ou é a linha
, ou é a linha ![]() de
de ![]() se
se ![]() .
.
[Demonstração do teorema ![]() ]
A prova segue da aplicação do algoritmo de eliminação de Gauss, fazendo-se uso do lema para se obter a factorização da forma
]
A prova segue da aplicação do algoritmo de eliminação de Gauss, fazendo-se uso do lema para se obter a factorização da forma ![]() , onde os pivots do algoritmo são o primeiro elemento não nulo de cada linha (não nula) de
, onde os pivots do algoritmo são o primeiro elemento não nulo de cada linha (não nula) de ![]() .
.
A característica de uma matriz ![]() , denotada por
, denotada por
![]() , por
, por ![]() ou ainda por
ou ainda por
![]() , é o número de linhas não nulas na matriz escada
, é o número de linhas não nulas na matriz escada ![]() obtida por aplicação do Algoritmo de Eliminação de Gauss. Ou seja, e sabendo que toda a linha não nula de
obtida por aplicação do Algoritmo de Eliminação de Gauss. Ou seja, e sabendo que toda a linha não nula de ![]() tem exactamente 1 pivot que corresponde ao primeiro elemento não nulo da linha, a característica de
tem exactamente 1 pivot que corresponde ao primeiro elemento não nulo da linha, a característica de ![]() é o número de pivots no algoritmo (ainda que o último possa não ser usado, por exemplo, no caso de estar na última linha). Note ainda que
é o número de pivots no algoritmo (ainda que o último possa não ser usado, por exemplo, no caso de estar na última linha). Note ainda que
![]() . Por exemplo,
. Por exemplo,
![$ \mathrm{car}\left[\begin{array}{cccc}
2 & 2 & 2 & 2\\
2 & 2 & 2 & 0\\
1 & 1 & 0 & 1\end{array}\right]=3$](img440.png) , já que a matriz escada obtida desta tem 3 linhas não nulas.
, já que a matriz escada obtida desta tem 3 linhas não nulas.
Uma matriz quadrada ![]() de ordem
de ordem ![]() diz-se não-singular se
diz-se não-singular se
![]() . Ou seja,
. Ou seja, ![]() é não-singular se forem usados
é não-singular se forem usados ![]() pivots no algoritmo de eliminação de Gauss. Uma matriz é singular se não for não-singular.
pivots no algoritmo de eliminação de Gauss. Uma matriz é singular se não for não-singular.
Por um lado, se ![]() é invertível, e como
é invertível, e como ![]() , segue que
, segue que ![]() é invertível, quadrada. Como
é invertível, quadrada. Como ![]() é triangular superior, não pode ter linhas nulas caso constrário teria um elemento diagonal nulo, o que contraria a invertibilidade de
é triangular superior, não pode ter linhas nulas caso constrário teria um elemento diagonal nulo, o que contraria a invertibilidade de ![]() .
.
Por outro lado, se ![]() é não-singular então
é não-singular então ![]() não tem linhas nulas. Como cada coluna de
não tem linhas nulas. Como cada coluna de ![]() tem no máximo 1 pivot, e existem
tem no máximo 1 pivot, e existem ![]() linhas e
linhas e ![]() pivots, então cada linha tem exactamente 1 pivot. Ou seja, os elementos diagonais de
pivots, então cada linha tem exactamente 1 pivot. Ou seja, os elementos diagonais de ![]() são não nulos. Como
são não nulos. Como ![]() é triangular superior, segue que
é triangular superior, segue que ![]() é invertível, e portanto
é invertível, e portanto ![]() é invertível visto
é invertível visto ![]() .
.
Octave
![\includegraphics[scale=0.3]{Octave_Sombrero.eps}](img64.png)
Ao se usar uma ferramenta computacional numérica é necessário algum cuidado nos erros de truncatura. Como exemplo, considere a matriz A=[1E-5 1E5; 1E5 1E-5]. Esta matriz é não-singular, e a única (porquê?) matriz escada obtida, sem quaisquer trocas de linhas, é
![$ \left[\begin{array}{cc}10^{-5}&10^5 0 & 10^{-5}-10^{15}\end{array}\right]$](img458.png) . Usando o Octave,
. Usando o Octave,
> format long
> E=eye (2); E(2,1)=-A(2,1)/A(1,1)
E =
1 0
-10000000000 1
> E*A
ans =
1.00000000000000e-05 1.00000000000000e+05
-1.45519152283669e-11 -1.00000000000000e+15
Repare que a matriz não é triangular inferior, e que o elemento > (E*A)(2,2)==-1E15 ans = 1 > -1E15==-1E15+1E-5 ans = 1Para o Octave, não existe distinção entre os dois números, por erro de arrondamento.
Embora o AEG seja pouco eficiente neste tipo de questões, existem algumas alterações que são efectuadas por forma a contornar este problema. Um exemplo é a pivotagem parcial. Este algoritmo será descrito com detalhe noutra unidade curricular de MiEB. A ideia é, quando se considera um pivot na entrada ![]() , percorrer os outros elementos que estão por baixo dele e trocar a linha
, percorrer os outros elementos que estão por baixo dele e trocar a linha ![]() com a linha do elemento que seja maior, em módulo. Tal corresponde a multiplicar, à esquerda, por uma matriz da forma
com a linha do elemento que seja maior, em módulo. Tal corresponde a multiplicar, à esquerda, por uma matriz da forma ![]() . Esse algorimto está implementado no Octave, sendo chamado pela instrução lu(A).
. Esse algorimto está implementado no Octave, sendo chamado pela instrução lu(A).
> [L,U,P]=lu (A) L = 1.000000000000000 0.000000000000000 0.000000000100000 1.000000000000000 U = 1.00000000000000e+05 1.00000000000000e-05 0.00000000000000e+00 1.00000000000000e+05 P = 0 1 1 0A matriz
> all(all(P*A==L*U)) ans = 1
![]()
![]()
![]()
![]()
Seguinte: Determinantes
Acima: Um resultado de factorização
Anterior: Matrizes elementares
Conteúdo
Pedro Patricio
2008-01-08