Resta-nos definir o produto matricial.
Seja
![]() uma matriz
uma matriz ![]() e
e
![]() uma matriz
uma matriz ![]() . O produto de
. O produto de ![]() por
por ![]() , denotado por
, denotado por ![]() , é a matriz
, é a matriz ![]() cujo elemento
cujo elemento ![]() é
é
![]() . Assim,
. Assim,
![$\displaystyle AB= \left[\sum_{k=1}^{p} a_{ik} b_{kj} \right]_{m \times p}$](img94.png) e portanto
e portanto 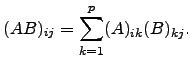
Atente-se nas dimensões de ![]() e
e ![]() na definição anterior.
na definição anterior.
Antes de fazermos referência a algumas propriedades, vejamos uma outra forma exprimir o produto de duas matrizes. Para tal, assuma que
![$ X=\left[\begin{array}{cccc}x_1&x_2&\dots &x_n\end{array}\right],Y=\left[\begin{array}{c}y_1 y_2 \vdots y_n\end{array}\right]$](img96.png) , sendo a primeira do tipo
, sendo a primeira do tipo ![]() e a segunda do tipo
e a segunda do tipo ![]() . Pelo que acabámos de referir, o produto de
. Pelo que acabámos de referir, o produto de ![]() por
por ![]() está bem definido, sendo a matriz produto do tipo
está bem definido, sendo a matriz produto do tipo ![]() , e portanto, um elemento de
, e portanto, um elemento de
![]() . Esse elemento é
. Esse elemento é
![]() . Voltemos agora ao produto de
. Voltemos agora ao produto de
![]() por
por
![]() , e fixemos a linha
, e fixemos a linha ![]() de
de ![]() e a coluna
e a coluna ![]() de
de ![]() . Ou seja, a matriz linha
. Ou seja, a matriz linha
![$ \left[\begin{array}{cccc}a_{i1}&a_{i2}&\dots&a_{ip}\end{array}\right]$](img105.png) e a matriz coluna
e a matriz coluna
![$ \left[\begin{array}{c}b_{1j} b_{2j} \vdots b_{pj}\end{array}\right]$](img106.png) . O produto da primeira pela segunda é o elemento de
. O produto da primeira pela segunda é o elemento de
![]() dado por
dado por
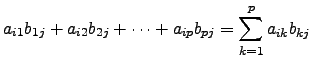 . Ora, este elemento não é mais nem menos que a entrada
. Ora, este elemento não é mais nem menos que a entrada ![]() da matriz produto
da matriz produto ![]() . Ou seja, a entrada
. Ou seja, a entrada ![]() de
de ![]() é o produto da linha
é o produto da linha ![]() de
de ![]() pela coluna
pela coluna ![]() de
de ![]() .
.
Vejamos algumas propriedades deste produto de matrizes, onde as dimensões das matrizes ![]() são tais que as operações indicadas estão definidas, e
são tais que as operações indicadas estão definidas, e
![]() :
:
Façamos a verificação da primeira igualdade de ![]() . A verificação de que as matrizes são do mesmo tipo fica ao cargo do leitor. Iremos apenas verificar que a entrada
. A verificação de que as matrizes são do mesmo tipo fica ao cargo do leitor. Iremos apenas verificar que a entrada ![]() de
de ![]() iguala a entrada
iguala a entrada ![]() de
de ![]() . Ora, supondo que
. Ora, supondo que ![]() tem
tem ![]() colunas, e portanto que
colunas, e portanto que ![]() e
e ![]() têm
têm ![]() linhas,
linhas,
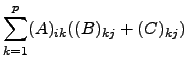 |
|||
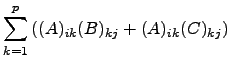 |
|||
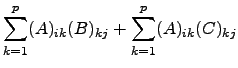 |
|||
Verifiquemos também a propriedade ![]() . Note-se que
. Note-se que ![]() e
e
![]() se
se ![]() . Ora
. Ora
![]() .
.
É importante notar que o produto matricial não é, em geral, comutativo. Por exemplo,
![$ \left[\begin{array}{cc}1 & 0 0&0\end{array}\right]\left[\begin{array}{cc}0&1...
...0&1 0&0\end{array}\right]\left[\begin{array}{cc}1 & 0 0&0\end{array}\right]$](img128.png) . A lei do anulamento do produto também não é válida, em geral, no produto matricial. Por exemplo,
. A lei do anulamento do produto também não é válida, em geral, no produto matricial. Por exemplo,
![$ \left[\begin{array}{cc}1 & 0 0&0\end{array}\right]\left[\begin{array}{cc}0&0 0&1\end{array}\right]=0$](img129.png) , sem que um dos factores seja nulo. Ou seja,
, sem que um dos factores seja nulo. Ou seja,
![]() . De uma forma mais geral,
. De uma forma mais geral,
![]() , já que, por exemplo,
, já que, por exemplo,
![$ \left[\begin{array}{cc}1 & 0 0&0\end{array}\right]\left[\begin{array}{cc}2&2...
... & 0 0&0\end{array}\right]\left[\begin{array}{cc}2&2 -1&3\end{array}\right]$](img132.png) .
.
Como é fácil de observar, a soma de duas matrizes triangulares inferiores [resp. triangulares superiores] é de novo triangular inferior [resp. triangular superior]. O que se pode dizer em relação ao produto?
Por vezes é conveniente considerar-se o produto matricial por blocos. Para tal, considere as matrizes ![]() e
e ![]() divididas em submatrizes
divididas em submatrizes
![$\displaystyle A=\left[\begin{array}{cc} A_{11}&A_{12} A_{21}&A_{22}\end{array...
...ht],
B=\left[\begin{array}{cc} B_{11}&B_{12} B_{21}&B_{22}\end{array}\right]$](img137.png)
![$\displaystyle AB=\left[\begin{array}{cc} A_{11}B_{11}+A_{12}B_{21} & A_{11}B_{1...
...22}\\
A_{21}B_{11}+A_{22}B_{21} & A_{21}B_{12}+A_{22}B_{22}\end{array}\right].$](img138.png)
![$\displaystyle A=\left[\begin{array}{cccc}
A_{11} & A_{12} & \cdots & A_{1p}\\
...
...vdots & \ddots & \vdots\\
B_{pn} & B_{pn} & \cdots & B_{pn} \end{array}\right]$](img139.png)
![$\displaystyle AB= \left[\begin{array}{cccc}
\sum_{k=1}^p A_{1k}B_{k1} & \sum_{k...
...sum_{k=1}^p A_{mk}B_{k2} & \cdots &\sum_{k=1}^p A_{mk}B_{kn}\end{array}\right].$](img140.png)