



Seguinte: Bases de espaços vectoriais
Acima: Espaços vectoriais
Anterior: Definição e exemplos
Conteúdo
Sejam  um espaço vectorial sobre
um espaço vectorial sobre
 e
e
 . Se
. Se
diz-se que  é uma combinação linear dos vectores
é uma combinação linear dos vectores
 . Neste caso, dizemos que
. Neste caso, dizemos que  se pode escrever como combinação linear de
se pode escrever como combinação linear de
 .
.
Definição 4.2.1 (Conjunto linearmente independente)
Um conjunto não vazio

diz-se
linearmente independente se
Um conjunto diz-se
linearmente dependente se não for linearmente independente.
Por abuso de linguagem, tomaremos, em algumas ocasiões, vectores linearmente independentes para significar que o conjunto formado por esses vectores é linearmente independente.
O conceito de dependência e independência linear é usualmente usado de duas formas.
- (i)
- Dado um conjunto não vazio
 de
de 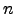 vectores linearmente dependentes, então é possível escrever o vector nulo como combinação linear não trivial de
vectores linearmente dependentes, então é possível escrever o vector nulo como combinação linear não trivial de
 . Ou seja, existem escalares
. Ou seja, existem escalares
 , algum ou alguns dos quais não nulos, tais que
Seja
, algum ou alguns dos quais não nulos, tais que
Seja  um coeficiente não nulo dessa combinação linear. Então
Concluindo, dado um conjunto de vectores linearmente dependentes, então pelo menos um desses vectores é uma combinação linear (não trivial) dos outros vectores.
um coeficiente não nulo dessa combinação linear. Então
Concluindo, dado um conjunto de vectores linearmente dependentes, então pelo menos um desses vectores é uma combinação linear (não trivial) dos outros vectores.
- (ii)
- Dado um conjunto não vazio
 de
de 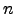 vectores linearmente independentes, da relação
podemos concluir de forma imediata e óbvia que
vectores linearmente independentes, da relação
podemos concluir de forma imediata e óbvia que
 . Esta implicação será muito útil ao longo desta disciplina.
. Esta implicação será muito útil ao longo desta disciplina.
Algumas observações:
- Considerando o espaço vectorial
![$ {\mathbb{K}}\left[x \right]$](img793.png) , o conjunto dos monómios
, o conjunto dos monómios
 é constituído por elementos linearmente independentes. Já
é constituído por elementos linearmente independentes. Já
 são linearmente dependentes, visto
são linearmente dependentes, visto
- Em
![$ {\mathbb{K}}_n \left[x \right]$](img759.png) , quaisquer
, quaisquer  polinómios são linearmente dependentes.
polinómios são linearmente dependentes.
- Em
 , consideremos os vectores
, consideremos os vectores
 . Estes quatro vectores são linearmente dependentes (pois
. Estes quatro vectores são linearmente dependentes (pois
 ), apesar de quaisquer três deles serem linearmente independentes.
), apesar de quaisquer três deles serem linearmente independentes.
Teorema 4.2.2
Sejam

elementos linearmente independentes de um espaço vectorial

. Sejam ainda

tais que
Então

, para todo

.
Se
 então
pelo que, usando o facto de
então
pelo que, usando o facto de
 serem linearmente independentes, se tem
serem linearmente independentes, se tem
 , para todo
, para todo
 .
.
O resultado anterior mostra a unicidade da escrita de um vector como combinação linear de elementos de um conjunto linearmente independente, caso essa combinação linear exista.
Teorema 4.2.3
Seja
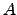
um subconjunto não vazio de um espaço vectorial

sobre

. Então o conjunto de todas as combinações lineares de elementos de
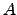
é um subespaço vectorial de

.
Seja  o conjunto de todas as combinações lineares de elementos de
o conjunto de todas as combinações lineares de elementos de 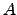 .
.  é obviamente não vazio visto
é obviamente não vazio visto
 . Sejam
. Sejam
 . Ou seja,
para alguns
. Ou seja,
para alguns
 , com
, com  . Note-se que
e portanto
. Note-se que
e portanto  é assim uma combinação linear de elementos de
é assim uma combinação linear de elementos de 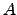 - logo,
- logo,
 . Para
. Para
 , temos que
, temos que
 e portanto
e portanto
 .
.
Tendo em conta o teorema anterior, podemos designar o conjunto das combinações lineares dos elementos de 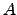 como o espaço gerado por
como o espaço gerado por 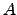 . Este espaço vectorial (subespaço de
. Este espaço vectorial (subespaço de  ) denota-se por
) denota-se por
 .
.
Quando o conjunto 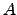 está apresentado em extensão, então não escrevemos as chavetas ao denotarmos o espaço gerado por esse conjunto. Por exemplo, se
está apresentado em extensão, então não escrevemos as chavetas ao denotarmos o espaço gerado por esse conjunto. Por exemplo, se
 , então
, então
 pode-se escrever como
pode-se escrever como
 .
Por notação,
.
Por notação,
 .
.
É importante referir os resultados que se seguem, onde  indica um espaço vectorial.
indica um espaço vectorial.
- Os vectores não nulos
 são linearmente independentes se e só se, para cada
são linearmente independentes se e só se, para cada 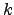 ,
,
 .
.
- Sejam
 .
.
- Se
 então
então
 .
.
-
 .
.
-
 é o menor (para a relação de ordem
é o menor (para a relação de ordem  ) subespaço de
) subespaço de  que contém
que contém 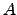 .
.




Seguinte: Bases de espaços vectoriais
Acima: Espaços vectoriais
Anterior: Definição e exemplos
Conteúdo
Pedro Patricio
2008-01-08
![]() um espaço vectorial sobre
um espaço vectorial sobre
![]() e
e
![]() . Se
. Se







![]() como o espaço gerado por
como o espaço gerado por ![]() . Este espaço vectorial (subespaço de
. Este espaço vectorial (subespaço de ![]() ) denota-se por
) denota-se por
![]() .
.
![]() está apresentado em extensão, então não escrevemos as chavetas ao denotarmos o espaço gerado por esse conjunto. Por exemplo, se
está apresentado em extensão, então não escrevemos as chavetas ao denotarmos o espaço gerado por esse conjunto. Por exemplo, se
![]() , então
, então
![]() pode-se escrever como
pode-se escrever como
![]() .
Por notação,
.
Por notação,
![]() .
.
![]() indica um espaço vectorial.
indica um espaço vectorial.
![]()
![]()
![]()
![]()