



Seguinte: Independência linear
Acima: Espaços vectoriais
Anterior: Espaços vectoriais
Conteúdo
Definição 4.1.1
Um conjunto não vazio

é um
espaço vectorial sobre

(ou espaço linear) se lhe estão associadas duas operações, uma adição de elementos de

e uma multiplicação de elementos de

por elementos de

, com as seguintes propriedades:
- Fecho da adição:
 ;
;
- Fecho da multiplicação por escalares:
 ;
;
- Comutatividade da adição:
 , para
, para  ;
;
- Associatividade da adição:
 , para
, para
 ;
;
- Existência de zero: existe um elemento de
 , designado por 0, tal que
, designado por 0, tal que  , para
, para  ;
;
- Existência de simétricos:
 ;
;
- Associatividade da multiplicação por escalares:
 ;
;
- Distributividade:
 e
e
 , para
, para  e
e
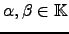 ;
;
- Existência de identidade:
 , para todo
, para todo  .
.
Se

é um espaço vectorial sobre

, um subconjunto não vazio

que é ele também um espaço vectorial sobre

diz-se um
subespaço vectorial de

.
Por forma a aligeirar a escrita, sempre que nos referirmos a um subespaço de um espaço vectorial queremos dizer subespaço vectorial.
Dependendo se o conjunto dos escalares
 é
é
 ou
ou
 , o espaço vectorial diz-se, respectivamente, real ou complexo.
, o espaço vectorial diz-se, respectivamente, real ou complexo.
Apresentam-se, de seguida, alguns exemplos comuns de espaços vectoriais.
- O conjunto
 das matrizes
das matrizes 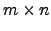 sobre
sobre
 , com a soma de matrizes e produto escalar definidos no início da disciplina, é um espaço vectorial sobre
, com a soma de matrizes e produto escalar definidos no início da disciplina, é um espaço vectorial sobre
 .
.
- Em particular,
 é um espaço vectorial.
é um espaço vectorial.
- O conjunto
 é um espaço vectorial.
é um espaço vectorial.
- O conjunto das sucessões de elementos de
 , com a adição definida por
, com a adição definida por
 e o produto escalar por
e o produto escalar por
 , é um espaço vectorial sobre
, é um espaço vectorial sobre
 . Este espaço vectorial é usualmente denotado por
. Este espaço vectorial é usualmente denotado por
 .
.
- Seja
![$ V={\mathbb{K}}\left[x \right]$](img758.png) o conjunto dos polinómios na indeterminada
o conjunto dos polinómios na indeterminada  com coeficientes em
com coeficientes em
 . Definindo a adição de vectores como a adição usual de polinómios e a multiplicação escalar como a multiplicação usual de um escalar por um polinómio,
. Definindo a adição de vectores como a adição usual de polinómios e a multiplicação escalar como a multiplicação usual de um escalar por um polinómio,  é um espaço vectorial sobre
é um espaço vectorial sobre
 .
.
- Dado
 , o conjunto
, o conjunto
![$ {\mathbb{K}}_n \left[x \right]$](img759.png) dos polinómios de grau inferior a
dos polinómios de grau inferior a 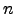 , com as operações definidas no exemplo anterior, é um espaço vectorial sobre
, com as operações definidas no exemplo anterior, é um espaço vectorial sobre
 .
.
- Seja
 o conjunto das aplicações de
o conjunto das aplicações de
 em
em
 (isto é,
(isto é,
 ). Definindo, para
). Definindo, para
 , a soma e produto escalar como as aplicações de
, a soma e produto escalar como as aplicações de
 em
em
 tais que, para
tais que, para
 ,
,
 é desta forma um espaço vectorial sobre
é desta forma um espaço vectorial sobre
 .
.
- O conjunto
 é um espaço vectorial sobre
é um espaço vectorial sobre
 .
.
 [resp.
[resp.
 ] é também um espaço vectorial sobre ele próprio.
] é também um espaço vectorial sobre ele próprio.
- Seja
 um espaço vectorial sobre
um espaço vectorial sobre
 e
e  um conjunto qualquer. O conjunto
um conjunto qualquer. O conjunto  de todas as funções de
de todas as funções de  em
em  é um espaço vectorial sobre
é um espaço vectorial sobre
 , com as operações
onde
, com as operações
onde
 .
.
- Dado um intervalo real
![$ ]a,b[$](img768.png) , o conjunto
, o conjunto ![$ C]a,b[$](img769.png) de todas as funções reais contínuas em
de todas as funções reais contínuas em ![$ ]a,b[$](img768.png) , para as operações habituais com as funções descritas acima, é um espaço vectorial sobre
, para as operações habituais com as funções descritas acima, é um espaço vectorial sobre
 . O conjunto
. O conjunto ![$ C^k]a,b[$](img770.png) das funções reais com derivadas contínuas até à ordem
das funções reais com derivadas contínuas até à ordem 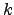 no intervalo
no intervalo ![$ ]a,b[$](img768.png) e o conjunto
e o conjunto
![$ C^{\infty} ]a,b[$](img771.png) das funções reais infinitamente diferenciáveis no intervalo
das funções reais infinitamente diferenciáveis no intervalo ![$ ]a,b[$](img768.png) são espaços vectoriais reais.
são espaços vectoriais reais.
Teorema 4.1.2
Seja

um espaço vectorial sobre

e

. Então

é um subespaço de

se e só se as condições seguintes forem satisfeitas:
-
 ;
;
-
 ;
;
-
 .
.
Observe que se  é subespaço de
é subespaço de  então necessariamente
então necessariamente  .
.
Alguns exemplos:
- Para qualquer
 ,
,
![$ C^\infty ]a,b[$](img777.png) é um subespaço de
é um subespaço de ![$ C^k]a,b[$](img770.png) , que por sua vez é um subespaço de
, que por sua vez é um subespaço de ![$ C]a,b[$](img769.png) .
.
- O conjunto das sucessões reais convergentes é um subespaço do espaço das sucessões reais.
-
![$ {\mathbb{K}}_n[x]$](img778.png) é um subespaço de
é um subespaço de
![$ {\mathbb{K}}[x]$](img779.png) .
.
- o conjunto das matrizes
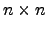 triangulares inferiores (inferiores ou superiores) é um subespaço de
triangulares inferiores (inferiores ou superiores) é um subespaço de
 , onde
, onde
 denota o espaço vectorial das matrizes quadradas de ordem
denota o espaço vectorial das matrizes quadradas de ordem 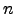 sobre
sobre
 .
.




Seguinte: Independência linear
Acima: Espaços vectoriais
Anterior: Espaços vectoriais
Conteúdo
Pedro Patricio
2008-01-08
 ;
;
 ;
;
 , para
, para  ;
;
 , para
, para
 ;
;
 , designado por 0, tal que
, designado por 0, tal que  , para
, para  ;
;
 ;
;
 ;
;
 e
e
 , para
, para  e
e
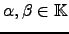 ;
;
 , para todo
, para todo  .
.