Nesta secção, vamos apresentar uma forma de resolução da equação ![]() , fazendo uso da factorização
, fazendo uso da factorização ![]() estudada atrás. Vejamos de que forma essa factorização é útil no estudo da equação.
estudada atrás. Vejamos de que forma essa factorização é útil no estudo da equação.
Considere a equação
![$ \left[\begin{array}{ccc} 1&2&3\\
0&4&5\\
0&0&6\end{array}\right]\left[\begin...
... x_2 x_3\end{array}\right]=\left[\begin{array}{c}7 8 9\end{array}\right]$](img624.png) . O sistema associado escreve-se como
. O sistema associado escreve-se como
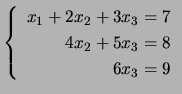 .
Calculando o valor de
.
Calculando o valor de ![]() pela última equação, este é substituido na segunda equação para se calcular o valor de
pela última equação, este é substituido na segunda equação para se calcular o valor de ![]() , que por sua vez são usados na primeira equação para se obter
, que por sua vez são usados na primeira equação para se obter ![]() . Procedeu-se à chamada substituição inversa para se calcular a única (repare que a matriz dada é invertível) solução do sistema. Em que condições se pode usar a substituição inversa? Naturalmente quando a matriz dada é triangular superior com elementos diagonais não nulos. Mas também noutros casos. Considere a equação matricial
. Procedeu-se à chamada substituição inversa para se calcular a única (repare que a matriz dada é invertível) solução do sistema. Em que condições se pode usar a substituição inversa? Naturalmente quando a matriz dada é triangular superior com elementos diagonais não nulos. Mas também noutros casos. Considere a equação matricial
![$ \left[\begin{array}{ccc} 1&2&3\\
0&0&4\end{array}\right]\left[\begin{array}{c}x_1 x_2 x_3\end{array}\right]=\left[\begin{array}{c}5 6\end{array}\right]$](img629.png) . A matriz do sistema não é quadrada, mas o método da susbstituição inversa pode ainda ser aplicado. O sistema associado é
. A matriz do sistema não é quadrada, mas o método da susbstituição inversa pode ainda ser aplicado. O sistema associado é
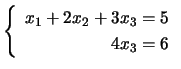 , donde
, donde
![]() , e
, e ![]() dependerá do valor de
dependerá do valor de ![]() . A solução geral do sistema é
. A solução geral do sistema é
![]() . Mais à frente veremos qual a importância de escrevermos a solução na última forma apresentada. É fácil constatar que a substituição inversa é aplicável desde que a matriz do sistema seja uma matriz escada de linhas. A estatégia na resolução da equação irá, portanto, passar pela matriz escada obtida por Gauss, para depois se aplicar a substituição inversa. Desde que o sistema seja possível, claro.
. Mais à frente veremos qual a importância de escrevermos a solução na última forma apresentada. É fácil constatar que a substituição inversa é aplicável desde que a matriz do sistema seja uma matriz escada de linhas. A estatégia na resolução da equação irá, portanto, passar pela matriz escada obtida por Gauss, para depois se aplicar a substituição inversa. Desde que o sistema seja possível, claro.
Considere o sistema ![]() e a factorização
e a factorização ![]() . Ou seja,
. Ou seja,
![]() . Recorde que
. Recorde que ![]() reflecte as operações elementares efectuadas nas linhas de
reflecte as operações elementares efectuadas nas linhas de ![]() por forma a se obter a matriz escada, percorrendo os passos do AEG. Multiplique ambos os membros de
por forma a se obter a matriz escada, percorrendo os passos do AEG. Multiplique ambos os membros de ![]() , à esquerda, por
, à esquerda, por ![]() para obter
para obter
![]() . Como
. Como
![]() tem-se que
tem-se que
![]() , e daqui podemos aplicar a substituição inversa... depois de se determinar o termo independente
, e daqui podemos aplicar a substituição inversa... depois de se determinar o termo independente ![]() . Recorde que
. Recorde que ![]() reflecte as operações elementares efectuadas nas linhas de
reflecte as operações elementares efectuadas nas linhas de ![]() , de modo que para se obter
, de modo que para se obter ![]() basta efectuar essas mesmas operações elementares, pela mesma ordem, nas linhas de
basta efectuar essas mesmas operações elementares, pela mesma ordem, nas linhas de ![]() . Por forma a simplificar o raciocínio e evitar possíveis enganos, esse processo pode ser efectuado ao mesmo tempo que aplicamos o AEG nas linhas de A. Consideramos, para esse efeito, a matriz aumentada do sistema
. Por forma a simplificar o raciocínio e evitar possíveis enganos, esse processo pode ser efectuado ao mesmo tempo que aplicamos o AEG nas linhas de A. Consideramos, para esse efeito, a matriz aumentada do sistema
![]() , aplicamos o AEG para se obter a matriz
, aplicamos o AEG para se obter a matriz
![]() , onde
, onde ![]() é matriz escada de linhas e
é matriz escada de linhas e
![]() . Se o sistema for possível, aplica-se a substituição inversa a
. Se o sistema for possível, aplica-se a substituição inversa a ![]() .
.
As soluções de ![]() são exactamente as mesmas de
são exactamente as mesmas de ![]() , e por este facto dizem-se equações equivalentes, e os sistemas associados são equivalentes. De facto, se
, e por este facto dizem-se equações equivalentes, e os sistemas associados são equivalentes. De facto, se ![]() é solução de
é solução de ![]() então
então ![]() , o que implica, por multiplicação à esquerda por
, o que implica, por multiplicação à esquerda por ![]() que
que
![]() , ou seja, que
, ou seja, que ![]() . Por outro lado, se
. Por outro lado, se ![]() então
então ![]() e portanto
e portanto ![]() . Ora
. Ora
![]() , e portanto
, e portanto ![]() . Obtemos então
. Obtemos então ![]() . Como
. Como ![]() é invertível, segue que
é invertível, segue que ![]() e
e ![]() é solução de
é solução de ![]() .
.
Visto determinar as soluções de ![]() é o mesmo que resolver
é o mesmo que resolver ![]() , interessa-nos, então classificar este último.
, interessa-nos, então classificar este último.
Como exemplo, considere a equação
![$ \left[\begin{array}{ccc}1&2&3\\
0&0&0\end{array}\right]\left[\begin{array}{c}x_1 x_2 x_3\end{array}\right]=\left[\begin{array}{c}4 5\end{array}\right]$](img648.png) . A segunda equação do sistema associado reflete a igualdade
. A segunda equação do sistema associado reflete a igualdade ![]() , o que é impossível. A equação é impossível já que não tem soluções. A matriz aumentada associada à equação é
, o que é impossível. A equação é impossível já que não tem soluções. A matriz aumentada associada à equação é
![$ \left[\begin{array}{ccc\vert c}
1&2&3&4\\
0&0&0&5\end{array}\right]$](img650.png) . Repare que a característica da matriz
. Repare que a característica da matriz ![]() é 1 enquanto que a caratacterística da matriz aumentada
é 1 enquanto que a caratacterística da matriz aumentada ![]() é 2.
é 2.
Como é fácil verificar, a característica da matriz a que se acrescentou linhas ou colunas é não inferior à característica da matriz inicial. Por consequência,
![]() .
.
Considere ![]() e
e
![]() . A equação
. A equação ![]() é equivalente à equação
é equivalente à equação ![]() , e portanto
, e portanto ![]() tem solução se e só se
tem solução se e só se ![]() tem solução. Tal equivale a dizer que o número de linhas nulas de
tem solução. Tal equivale a dizer que o número de linhas nulas de ![]() iguala o número de linhas nulas de
iguala o número de linhas nulas de ![]() . De facto, o número sendo o mesmo, por substituição inversa é possível obter uma solução de
. De facto, o número sendo o mesmo, por substituição inversa é possível obter uma solução de ![]() , e caso o número seja distinto então obtemos no sistema associado a igualdade
, e caso o número seja distinto então obtemos no sistema associado a igualdade ![]() , para algum
, para algum ![]() , o que torna
, o que torna ![]() impossível. Se o número de linhas nulas de
impossível. Se o número de linhas nulas de ![]() iguala o de
iguala o de ![]() então o número de linhas não nulas de
então o número de linhas não nulas de ![]() iguala o de
iguala o de ![]() .
.
Octave
![\includegraphics[scale=0.3]{Octave_Sombrero.eps}](img64.png)
Considere a equação matricial ![]() onde
onde
![$ A=\left[\begin{array}{ccc}
2& 2& 1\\
1& 1 & \frac{1}{2}\end{array}\right]$](img657.png) e
e
![$ b=\left[\begin{array}{c}
-1 1\end{array}\right]$](img658.png) . A equação é consistente se e só se
. A equação é consistente se e só se
![]()
> A=[2 2 1; 1 1 0.5]; b=[-1; 1];
> rank(A)
ans = 1
> [L,U,P]=lu(A)
L =
1.00000 0.00000
0.50000 1.00000
U =
2 2 1
0 0 0
P =
1 0
0 1
Portanto,
![]() .
.
> rank([A b])
ans = 2
> Aaum =
2.00000 2.00000 1.00000 -1.00000
1.00000 1.00000 0.50000 1.00000
> [Laum,Uaum,Paum]=lu(Aaum)
Laum =
1.00000 0.00000
0.50000 1.00000
Uaum =
2.00000 2.00000 1.00000 -1.00000
0.00000 0.00000 0.00000 1.50000
Paum =
1 0
0 1
Ora a caraterística da matriz aumentada é 2, pelo que ![]() é inconsistente.
é inconsistente.
Dada a equação
![$ A\left[\begin{array}{c}x_1 x_2 \vdots x_n \end{array}\right]=b$](img661.png) , considere
, considere
![$ U\left[\begin{array}{c}x_1 x_2 \vdots x_n \end{array}\right]=c$](img662.png) equivalente à primeira fazendo uso da factorização
equivalente à primeira fazendo uso da factorização ![]() da forma habitual. A incógnita
da forma habitual. A incógnita ![]() diz-se incógnita básica se a coluna
diz-se incógnita básica se a coluna ![]() de
de ![]() tem pivot. Uma incógnita diz-se livre se não for básica. A nulidade de
tem pivot. Uma incógnita diz-se livre se não for básica. A nulidade de ![]() ,
,
![]() , é o número de incógnitas livres na resolução de
, é o número de incógnitas livres na resolução de ![]() .
.
Octave
![\includegraphics[scale=0.3]{Octave_Sombrero.eps}](img64.png)
Na equação ![]() , com
, com
![$ A=\left[\begin{array}{ccc} 2 & 2 & 1 1 & 1 & -1\end{array}\right],x= \left[\...
...x_2 x_3 \end{array}\right],b=\left[\begin{array}{c}-1 1 \end{array}\right]$](img665.png) , obtemos a decomposição
, obtemos a decomposição
> A=[2 2 1; 1 1 -1]; b=[-1; 1]; > [L,U,P]=lu(A) L = 1.00000 0.00000 0.50000 1.00000 U = 2.00000 2.00000 1.00000 0.00000 0.00000 -1.50000 P = 1 0 0 1
Repare que
![]() . Ora
. Ora
![]() , já que a característica de uma matriz é não superior ao seu número de linhas e ao seu número de colunas. Segue que
, já que a característica de uma matriz é não superior ao seu número de linhas e ao seu número de colunas. Segue que
![]() . A equação
. A equação ![]() é, portanto, consistente. Façamos, então, a classificação das incógnitas
é, portanto, consistente. Façamos, então, a classificação das incógnitas
![]() em livres e em básicas. Atente-se à matriz escada de linhas
em livres e em básicas. Atente-se à matriz escada de linhas ![]() apresentada atrás. As colunas
apresentada atrás. As colunas ![]() e
e ![]() têm como pivots, respectivamente,
têm como pivots, respectivamente, ![]() e
e
![]() . As incógnitas
. As incógnitas ![]() e
e ![]() são básicas. Já
são básicas. Já ![]() é livre pois a coluna
é livre pois a coluna ![]() de
de ![]() não tem pivot.
não tem pivot.
Qual o interesse neste tipo de classificação das incógnitas? A explicação é feita à custa do exemplo anterior. A equação ![]() é equivalente à equação
é equivalente à equação ![]() , com
, com
![$ U=\left[\begin{array}{ccc} 2 &2&1 0&0&-\frac{3}{2}\end{array}\right],c=\left[\begin{array}{c}-1 \frac{3}{2}\end{array}\right]$](img671.png) .
.
Octave
![\includegraphics[scale=0.3]{Octave_Sombrero.eps}](img64.png)
Com os dados fornecidos,
> [Laum,Uaum,Paum]=lu([A b]) Laum = 1.00000 0.00000 0.50000 1.00000 Uaum = 2.00000 2.00000 1.00000 -1.00000 0.00000 0.00000 -1.50000 1.50000 Paum = 1 0 0 1
Podemos, agora, aplicar o método da substituição inversa para obter as soluções da equação. Esse método é aplicado da seguinte forma:
Para conveniência futura, a solução é apresentada na forma
![$\displaystyle \left[\begin{array}{c}
x_1 x_2 \vdots x_n \end{array}\righ...
...]+ \dots
x_{i_k} \left[\begin{array}{c} ? ? \vdots ? \end{array}\right]$](img673.png)
Voltando ao exemplo, recorde que se obteve a equação equivalente à dada
![$\displaystyle \left[\begin{array}{ccc} 2 &2&1 0&0&-\frac{3}{2}\end{array}\rig...
...x_3\end{array}\right]=\left[\begin{array}{c}-1 \frac{3}{2}\end{array}\right].$](img675.png)
Num sistema possível, a existência de incógnitas livres confere-lhe a existência de várias soluções, e portanto o sistema é possível indeterminado. Ora, se o número de incógnitas é ![]() e se
e se ![]() delas são básicas, então as restantes
delas são básicas, então as restantes ![]() são livres. Recorde que o número de incógnitas iguala o número de colunas da matriz do sistema, e que a característica de uma matriz é igual ao número de pivots. Existindo, no máximo, um pivot por coluna, e como o número das colunas com pivots é igual ao número de incógnitas básicas, segue que a característica da matriz é igual ao número de incógnitas básicas. A existência de incógnitas livres é equivalente ao facto de existirem colunas sem pivot, ou seja, do número de colunas ser estritamente maior que a característica da matriz. De facto, as incógnitas livres são, em número, igual ao número de colunas sem pivot.
são livres. Recorde que o número de incógnitas iguala o número de colunas da matriz do sistema, e que a característica de uma matriz é igual ao número de pivots. Existindo, no máximo, um pivot por coluna, e como o número das colunas com pivots é igual ao número de incógnitas básicas, segue que a característica da matriz é igual ao número de incógnitas básicas. A existência de incógnitas livres é equivalente ao facto de existirem colunas sem pivot, ou seja, do número de colunas ser estritamente maior que a característica da matriz. De facto, as incógnitas livres são, em número, igual ao número de colunas sem pivot.
Recorde que o número de incógnitas livres é o número de colunas sem pivot na resolução de um sistema possível ![]() . Por outro lado, a nulidade de
. Por outro lado, a nulidade de ![]() ,
,
![]() , é o número de incógnitas livres que surgem na resolução de
, é o número de incógnitas livres que surgem na resolução de ![]() . Recorde ainda que a característica de
. Recorde ainda que a característica de ![]() ,
,
![]() , é o número de pivots na implementação de Gauss, que por sua vez é o número de colunas com pivot, que iguala o número de incógnitas básicas na equação
, é o número de pivots na implementação de Gauss, que por sua vez é o número de colunas com pivot, que iguala o número de incógnitas básicas na equação ![]() . Como o número de colunas de uma matriz iguala o número de incógnitas equação
. Como o número de colunas de uma matriz iguala o número de incógnitas equação ![]() , e estas se dividem em básicas e em livres, correspondendo em número a, respectivamente,
, e estas se dividem em básicas e em livres, correspondendo em número a, respectivamente,
![]() e
e
![]() , temos o resultado seguinte:
, temos o resultado seguinte:
O resultado seguinte descreve as soluções de uma equação possível ![]() à custa do sistema homogéneo associado (ou seja,
à custa do sistema homogéneo associado (ou seja, ![]() ) e de uma solução particular
) e de uma solução particular ![]() de
de ![]() .
.
Reciprocamente, assuma ![]() solução de
solução de ![]() e
e ![]() solução de
solução de ![]() . Pretende-se mostrar que
. Pretende-se mostrar que ![]() é solução de
é solução de ![]() . Para tal,
. Para tal,
![]() .
.
Ou seja, conhecendo o conjunto das soluções de ![]() e uma solução particular de
e uma solução particular de ![]() , conhece-se o conjunto das soluções de
, conhece-se o conjunto das soluções de ![]() .
.
Octave
![\includegraphics[scale=0.3]{Octave_Sombrero.eps}](img64.png)
Considere a equação matricial ![]() , com
, com
![$ A=\left[\begin{array}{ccc}
9 & -2 & 4 \\
6 & -5 & 0 \\
-12 & -1 & -8 \end{array}\right]$](img692.png) e
e
![$ b=\left[\begin{array}{c} 3 5 -1\end{array}\right]$](img693.png) . O sistema é consistente, já que
. O sistema é consistente, já que
![]() :
:
> rank ([A b]) ans = 2 > rank (A) ans = 2Sendo a característica de
> [Laum,Uaum,Paum]=lu([A b])
Laum =
1.00000 0.00000 0.00000
-0.50000 1.00000 0.00000
-0.75000 0.50000 1.00000
Uaum =
-12.00000 -1.00000 -8.00000 -1.00000
0.00000 -5.50000 -4.00000 4.50000
0.00000 0.00000 0.00000 0.00000
Paum =
0 0 1
0 1 0
1 0 0
Se
Como vimos do resultado anterior, conhecendo uma solução particular de ![]() , digamos,
, digamos, ![]() , e conhecendo
, e conhecendo ![]() , ou seja, o conjunto das soluções de
, ou seja, o conjunto das soluções de ![]() , então as soluções de
, então as soluções de ![]() são da forma
são da forma ![]() , onde
, onde ![]() . Uma solução particular pode ser encontrada tomando a incógnita livre como zero. Ou seja, considerando
. Uma solução particular pode ser encontrada tomando a incógnita livre como zero. Ou seja, considerando ![]() . A sunbstituição inversa fornece o valor das incógnitas básicas
. A sunbstituição inversa fornece o valor das incógnitas básicas ![]() :
:
> x2=Uaum(2,4)/Uaum(2,2) x2 = -0.81818 > x1=(Uaum(1,4)-Uaum(1,2)*x2)/Uaum(1,1) x1 = 0.15152
Este passo pode ser efectuado, de uma forma mais simples, como
> A\b ans = 0.31235 -0.62518 -0.26538Resta-nos determinar
> null (A) ans = 0.44012 0.52814 -0.72620
O vector ![]() que nos é indicado significa que
que nos é indicado significa que ![]() é formado por todas a colunas da forma
é formado por todas a colunas da forma ![]() . Se, por ventura, nos forem apresentados vários vectores v1 v2 ... vn, então os elementos de
. Se, por ventura, nos forem apresentados vários vectores v1 v2 ... vn, então os elementos de ![]() escrevem-se da forma
escrevem-se da forma
![]() .
.
Considere, agora, a matriz
> A=[2 2 2 0; 1 1 2 2];Esta matriz tem característica 2, como se pode verificar à custa da factorização
> [L,U,P]=lu(A) L = 1.00000 0.00000 0.50000 1.00000 U = 2 2 2 0 0 0 1 2 P = 1 0 0 1A nulidade é 2, pelo que existem 2 incógnitas livres na resolução de
![$ A\left[\begin{array}{cccc} x_1 & x_2 & x_3 & x_4\end{array}\right]^T =0_{2\times 1}$](img701.png) . As incógnitas livres são as correspondentes à colunas de
. As incógnitas livres são as correspondentes à colunas de 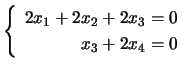 . Resolvendo o sistema em relação à incógnitas básicas
. Resolvendo o sistema em relação à incógnitas básicas Sem nos alongarmos em demasia neste assunto, o Octave, como já foi referido, contém uma instrução que calcula o núcleo de uma matriz:
> null(A) ans = -0.71804 -0.35677 0.10227 0.79524 0.61577 -0.43847 -0.30788 0.21924O resultado apresentado indica os vectores que decrevem o conjunto
> null(A)(:,1)'*null(A)(:,2) ans = 6.2694e-17 > null(A)(:,1)'*null(A)(:,1) ans = 1.0000 > null(A)(:,2)'*null(A)(:,2) ans = 1
![]()
![]()
![]()
![]()
Seguinte: Algoritmo de Gauss-Jordan
Acima: Sistemas de equações lineares
Anterior: Formulação matricial
Conteúdo
Pedro Patricio
2008-01-08