next up previous contents
Seguinte: Transposição Acima: Operações matriciais Anterior: Soma e produto escalar   Conteúdo

Produto

Resta-nos definir o produto matricial.

Seja $ A= \left[a_{ij} \right]$ uma matriz $ m\times p$ e $ B=\left[b_{ij} \right]$ uma matriz $ p\times n$ . O produto de $ A$ por $ B$ , denotado por $ AB$ , é a matriz $ m \times n$ cujo elemento $ (i,j)$ é $ a_{i1} b_{1j} + a_{i2} b_{2j} + \cdots + a_{in} b_{nj}$ . Assim,

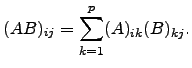
$\displaystyle AB= \left[\sum_{k=1}^{p} a_{ik} b_{kj} \right]_{m \times p}$    e portanto $\displaystyle (AB)_{ij}=\sum_{k=1}^{p} (A)_{ik} (B)_{kj}.$

Atente-se nas dimensões de $ A$ e $ B$ na definição anterior.

Antes de fazermos referência a algumas propriedades, vejamos uma outra forma exprimir o produto de duas matrizes. Para tal, assuma que $ X=\left[\begin{array}{cccc}x_1&x_2&\dots &x_n\end{array}\right],Y=\left[\begin{array}{c}y_1\\ y_2\\ \vdots \\ y_n\end{array}\right]$ , sendo a primeira do tipo $ 1\times n$ e a segunda do tipo $ n\times 1$ . Pelo que acabámos de referir, o produto de $ X$ por $ Y$ está bem definido, sendo a matriz produto do tipo $ 1\times 1$ , e portanto, um elemento de $ {\mathbb{K}}$ . Esse elemento é $ x_1y_1+x_2y_2+\dots x_ny_n$ . Voltemos agora ao produto de $ A_{m\times p}$ por $ B_{p\times n}$ , e fixemos a linha $ i$ de $ A$ e a coluna $ j$ de $ B$ . Ou seja, a matriz linha $ \left[\begin{array}{cccc}a_{i1}&a_{i2}&\dots&a_{ip}\end{array}\right]$ e a matriz coluna $ \left[\begin{array}{c}b_{1j}\\ b_{2j}\\ \vdots \\ b_{pj}\end{array}\right]$ . 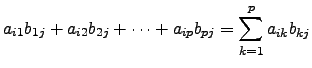O produto da primeira pela segunda é o elemento de $ {\mathbb{K}}$ dado por $ a_{i1}b_{1j}+a_{i2}b_{2j}+\cdots +a_{ip}b_{pj}=\displaystyle\sum_{k=1}^p a_{ik} b_{kj}$ . Ora, este elemento não é mais nem menos que a entrada $ (i,j)$ da matriz produto $ AB$ . Ou seja, a entrada $ (i,j)$ de $ AB$ é o produto da linha $ i$ de $ A$ pela coluna $ j$ de $ B$ .

Vejamos algumas propriedades deste produto de matrizes, onde as dimensões das matrizes $ A,B,C,I,0$ são tais que as operações indicadas estão definidas, e $ \alpha \in {\mathbb{K}}$ :

  1. O produto de matrizes é associativo $ (AB)C=A(BC)$ ;
  2. O produto de matrizes é distributivo em relação à soma $ A(B+C)=AB+AC,(A+B)C=AC+BC$ ;
  3. A matriz identidade é o elemento neutro para o produto: $ AI=A, IA=A$ ;
  4. A matriz nula é o elemento absorvente para o produto: $ 0A=0,A0=0$ ;
  5. $ \alpha (AB)=(\alpha A)B = A (\alpha B)$ .

Façamos a verificação da primeira igualdade de $ (1)$ . A verificação de que as matrizes são do mesmo tipo fica ao cargo do leitor. Iremos apenas verificar que a entrada $ (i,j)$ de $ A(B+C)$ iguala a entrada $ (i,j)$ de $ AB+AC$ . Ora, supondo que $ A$ tem $ p$ colunas, e portanto que $ B$ e $ C$ têm $ p$ linhas,

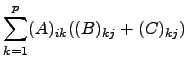$\displaystyle (A(B+C))_{ij}$ $\displaystyle =$ $\displaystyle \sum_{k=1}^p (A)_{ik}((B)_{kj}+(C)_{kj})$  
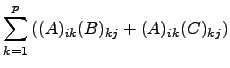  $\displaystyle =$ $\displaystyle \sum_{k=1}^p \left((A)_{ik}(B)_{kj}+(A)_{ik}(C)_{kj}\right)$  
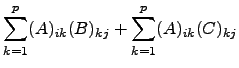  $\displaystyle =$ $\displaystyle \sum_{k=1}^p (A)_{ik}(B)_{kj}+\sum_{k=1}^p(A)_{ik}(C)_{kj}$  
  $\displaystyle =$ $\displaystyle (AB)_{ij}+(AC){ij}=(AB+AC)_{ij}.$  

Verifiquemos também a propriedade $ (3)$ . Note-se que $ (I)_{i}=1 $ e $ (I)_{ij}= 0$ se $ i \ne j$ . Ora $ (AI)_{ij}=\sum_{k=1}^p (A)_{ik} (I)_{kj}=(A)_{ij}$ .

É importante notar que o produto matricial não é, em geral, comutativo. Por exemplo, $ \left[\begin{array}{cc}1 & 0\\ 0&0\end{array}\right]\left[\begin{array}{cc}0&1... ...0&1\\ 0&0\end{array}\right]\left[\begin{array}{cc}1 & 0\\ 0&0\end{array}\right]$ . A lei do anulamento do produto também não é válida, em geral, no produto matricial. Por exemplo, $ \left[\begin{array}{cc}1 & 0\\ 0&0\end{array}\right]\left[\begin{array}{cc}0&0\\ 0&1\end{array}\right]=0$ , sem que um dos factores seja nulo. Ou seja, $ AB=0 \nRightarrow \left( A=0 \text{ ou } B=0\right)$ . De uma forma mais geral, $ \left(AB=AC \text{ e } A \ne 0 \right) \nRightarrow \left( B=C \right)$ , já que, por exemplo, $ \left[\begin{array}{cc}1 & 0\\ 0&0\end{array}\right]\left[\begin{array}{cc}2&2... ... & 0\\ 0&0\end{array}\right]\left[\begin{array}{cc}2&2\\ -1&3\end{array}\right]$ .

Como é fácil de observar, a soma de duas matrizes triangulares inferiores [resp. triangulares superiores] é de novo triangular inferior [resp. triangular superior]. O que se pode dizer em relação ao produto?

Teorema 1.2.1   O produto de matrizes triangulares inferiores [resp. triangulares superiores] é de novo uma matriz triangular inferior [resp. triangular superior].

Sejam $ A,B$ duas matrizes triangulares inferiores de tipo apropriado. Ou seja, $ (A)_{ij},(B)_{ij}=0$ , para $ i<j$ . Pretende-se mostrar que, para $ i<j$ se tem $ (AB)_{ij}=0$ . Ora, para $ i<j$ , e supondo que $ A$ tem $ p$ colunas, $ (AB)_{ij}= \sum_{k=1}^p (A)_{ik}(B)_{kj}=\sum_{k=1}^i (A)_{ik}(B)_{kj}=0$ .

Por vezes é conveniente considerar-se o produto matricial por blocos. Para tal, considere as matrizes $ A$ e $ B$ divididas em submatrizes

$\displaystyle A=\left[\begin{array}{cc} A_{11}&A_{12}\\ A_{21}&A_{22}\end{array... ...ht], B=\left[\begin{array}{cc} B_{11}&B_{12}\\ B_{21}&B_{22}\end{array}\right]$

de forma conforme as operações descritas de seguida estejam definidas, então

$\displaystyle AB=\left[\begin{array}{cc} A_{11}B_{11}+A_{12}B_{21} & A_{11}B_{1... ...22}\\ A_{21}B_{11}+A_{22}B_{21} & A_{21}B_{12}+A_{22}B_{22}\end{array}\right].$

De uma forma mais geral, se

$\displaystyle A=\left[\begin{array}{cccc} A_{11} & A_{12} & \cdots & A_{1p}\\ ... ...vdots & \ddots & \vdots\\ B_{pn} & B_{pn} & \cdots & B_{pn} \end{array}\right]$

em que as submatrizes são tais que as operações seguintes estão bem definidas, então

$\displaystyle AB= \left[\begin{array}{cccc} \sum_{k=1}^p A_{1k}B_{k1} & \sum_{k... ...sum_{k=1}^p A_{mk}B_{k2} & \cdots &\sum_{k=1}^p A_{mk}B_{kn}\end{array}\right].$

next up previous contents
Seguinte: Transposição Acima: Operações matriciais Anterior: Soma e produto escalar   Conteúdo
pedro 2007-05-29