Sistemas de equações lineares

Uma equação linear em $n$ variáveis $x_1,\dots ,x_n$ sobre ${\mathbb{K}}$ é uma equação da forma

$$a_1x_1+a_2x_2+\dots +a_n x_n=b,$$

onde $a_1,a_2,\dots ,a_n,b\in {\mathbb{K}}$ . Um sistema de equações lineares é um conjunto finito de equações lineares que é resolvido simultaneamente. Ou seja, que se pode escrever da forma

$$\left\{ \begin{array}{rcl} a_{11}x_1 + \dots +a_{1n}x_n & = & b_1... ...(1) \\ \cdots &&\\ a_{m1}x_1 + \dots +a_{mn}x_n & = & b_m \end{array}\right.$$

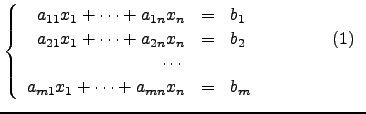
Este tipo de sistema pode ser representado na forma matricial

$$Ax=b,$$

com

$$A=\left[\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n}\\ ... ...ght], b= \left[\begin{array}{c} b_1\\ b_2\\ \vdots \\ b_m \end{array}\right].$$

$A$ é a matriz do sistema, $x$ é a coluna das incógnitas e $b$ é a coluna dos termos independentes, também denominado por segundo membro do sistema.

De ora em diante não faremos distinção entre o sistema de equações lineares e a sua formulação matricial $Ax=b$ .

Neste capítulo, vamo-nos debruçar sobre a resolução deste tipo de equação. Dizemos que $v$ é solução de $Ax=b$ se $Av=b$ , ou seja, quando $v$ é uma realização possível para a coluna das incógnitas. Iremos ver em que condições a equação tem solução, e como se podem determinar. Entende-se por resolver o sistema $Ax=b$ encontrar o conjunto (ainda que vazio) de todas as realizações possíveis para a coluna das incógnitas. O sistema diz-se impossível ou inconsistente se o conjunto é vazio e possível ou consistente caso contrário. Neste último caso, diz-se que é possível determinado se existir apenas um e um só elemento no conjunto das soluções, e possível indeterminado se for possível mas existirem pelo menos duas soluções distintas^2.1. Entende-se por classificar o sistema a afirmação em como ele é impossível, possível determinada ou possível indeterminado.

Um caso particular da equação $Ax=b$ surge quando $b=0$ . Ou seja, quando a equação é da forma $Ax=0$ . O sistema associado a esta equação chama-se sistema homogéneo. Repare que este tipo de sistema é sempre possível. De facto, o vector nulo (ou seja, a coluna nula) é solução. Ao conjunto das soluções de $Ax=0$ chamamos núcleo^2.2 de $A$ , e é denotado por $N(A)$ ou ainda por $\ker(A)$ . Ou seja, para $A$ do tipo $m \times n$ ,

$$N(A)=\ker(A)=\left\{ x\in {\mathbb{K}}^n: Ax=0_{m\times 1} \right\}.$$

Pelo que acabámos de referir, e independentemente da escolha de $A$ , o conjunto $\ker(A)$ é sempre não vazio já que $0_{n\times 1} \in \ker(A)$ .

Ou caso relevante no estudo da equação $Ax=b$ surge quando a matriz $A$ é invertível. Neste caso, multpiplicando ambos os membros de $Ax=b$ , à esquerda, por $A^{-1}$ , obtemos $A^{-1}Ax=A^{-1}b$ , e portanto $x=A^{-1}b$ . Ou seja, a equação é possível determinada, sendo $A^{-1}b$ a sua única solução.