Definição

Considere a matriz $A=\left[\begin{array}{cc} a & b\\ c & d\end{array}\right]$ e assuma $a\ne 0$ Aplicando Gauss, obtemos a factorização $\left[\begin{array}{cc} 1& 0\\ -\frac{c}{a} & 1 \end{array}\right]\left[\begi... ...ay}\right]=\left[\begin{array}{cc} a&b\\ 0 & -\frac{bc}{a}+d\end{array}\right]$ . Ou seja, a matriz $A$ é aquivalente por linhas à matriz $U= \left[\begin{array}{cc} a&b\\ 0 & -\frac{bc}{a}+d\end{array}\right]$ , que é uma matriz triangular superior. Recorde que $A$ é invertível se e só se $U$ for invertível. Ora, a matriz $U$ é invertível se e só se $-\frac{bc}{a}+d\ne 0$ , ou de forma equivalente, se $ad-bc\ne 0$ . Portanto, $A$ é invertível se e só se $ad-bc\ne 0$ .

Este caso simples serve de motivação para introduzir a noção de determinante de uma matriz.

Na definição que se apresenta de seguida, $S_n$ indica o grupo simétrico (ver Definição 1.3.1).

Definição 1.4.1   Seja $A$ uma matriz quadrada de ordem $n$ . O determinante de $A$ , denotado por $\det A$ ou $\vert A\vert$ , é o escalar definido por

$$\sum _{\sigma\in S_n} sgn(\sigma)\, a_{1\sigma(1)}a_{2\sigma(2)}\cdots a_{n\sigma(n)}.$$

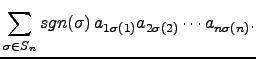
Vejamos os que resulta da fórmula, quando consideramos matrizes $2\times 2$ e matrizes $3\times 3$ .

Seja $A=\left[\begin{array}{cc} a_{11} & a_{12}\\ a_{21}&a_{22}\end{array}\right]$ . Neste caso, o grupo simétrico $S_2$ tem apenas as permutações $\sigma_1=(1\, 2)$ e $\sigma_2=(2\, 1)$ , sendo que $sgn(\sigma_1)=1$ e que $sgn(\sigma_2)=-1$ . Recorde que $\sigma_1(1)=1,\sigma_1(2)=2,\sigma_2(1)=2$ e $\sigma_2(2)=1$ . Obtemos, então, $\vert A\vert=a_{11}a_{22}-a_{12}a_{21}$ .

Figura: Esquema do cálculo do determinante de matrizes de ordem 2

Seja agora $A=\left[\begin{array}{ccc} a_{11} &a_{12} &a_{13} \\ a_{21} &a_{22} &a_{23} \\ a_{31} &a_{32} &a_{33}\end{array}\right]$ . Recorde que $S_3$ tem 6 elementos. No quadro seguinte, indicamos, respectivamente, a permutação $\sigma \in S_3$ , o seu sinal, e o produto $a_{1\sigma(1)}a_{2\sigma(2)}\cdots a_{n\sigma(n)}$ .

Permutação $\sigma \in S_3$	$sgn(\sigma)$	$a_{1\sigma(1)}a_{2\sigma(2)}\cdots a_{n\sigma(n)}$
$(1\, 2\, 3)$	$+1$	$a_{11}a_{22}a_{33}$
$(2\, 3\, 1)$	$+$ 1	$a_{12}a_{23}a_{31}$
$(3\, 1\, 2)$	$+1$	$a_{13}a_{21}a_{32}$
$(1\, 3\, 2)$	$-1$	$a_{11}a_{23}a_{32}$
$(2\, 1\, 3)$	$-1$	$a_{12}a_{21}a_{33}$
$(3\, 2\, 1)$	$-1$	$a_{11}a_{22}a_{31}$

Obtemos, assim,

$$\vert A\vert = a_{11}a_{22}a_{33}+ a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}$$

$$-a_{11}a_{23}a_{32} -a_{12}a_{21}a_{33} - a_{11}a_{22}a_{31}$$

Para fácil memorização, pode-se recorrer ao esquema apresentado de seguida.

Figura: Esquema do cálculo do determinante de matrizes de ordem 3, ou a Regra de Sarrus