



Seguinte: Grafos eulerianos e grafos
Acima: Breve introdução à teoria
Anterior: Caminhos e conexidade
Conteúdo
Um grafo diz-se planar se for possível desenhá-lo de tal forma que duas arestas não se intersectem à excepção nos vértices inicial e final. Por exemplo, o cubo é um grafo planar já que pode ser desenhado como
Outro exemplo de grafo planar é 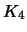 (verifique!), e o objectivo desta secção é caracterizar tais grafos. Um resultado relevante no estudo da planaridade de grafos é o Teorema de Kuratowski, que passamos a enunciar:
(verifique!), e o objectivo desta secção é caracterizar tais grafos. Um resultado relevante no estudo da planaridade de grafos é o Teorema de Kuratowski, que passamos a enunciar:
Um grafo é planar se e só se não tem nenhum subgrafo homeomorfo a 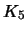 ou
ou 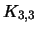 .
.
Antes de compreendermos o enunciado, é importante apresentar mais definições e alguns resultados.
Um grafo planar divide o plano em regiões, à custa das suas arestas. Cada uma destas divisões é denominada por face do grafo. Dois pontos do plano estão na mesma face se existir uma curva do plano que os une sem intersectar nenhuma das arestas do grafo. No grafo apresentado atrás, existem 6 faces (a face ``exterior'' é contabilizada! - esta é denominada por face infinita, ou face exterior). A fronteira de uma face, 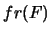 , é o conjunto das arestas que delimitam a face
, é o conjunto das arestas que delimitam a face 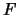 , ou que estão contidas em
, ou que estão contidas em 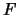 .
.
Teorema 6.1 (Fórmula de Euler)
Dado um grafo planar conexo
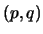
com
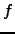
faces,
Se 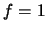 então o grafo é acíclico, e sendo conexo segue que é uma árvore. Como foi provado na secção anterior,
então o grafo é acíclico, e sendo conexo segue que é uma árvore. Como foi provado na secção anterior, 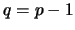 e a fórmula é válida.
e a fórmula é válida.
Suponhamos agora que 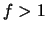 ; a igualdade é provada por indução sobre o número de arestas.
; a igualdade é provada por indução sobre o número de arestas.
Se 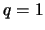 então
então 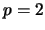 e
e 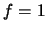 , ou então
, ou então 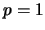 , e portanto
, e portanto 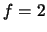 . Uma representação destes dois casos é, respectivamente,
. Uma representação destes dois casos é, respectivamente,
Em qualquer um dos casos, a fórmula é válida quando 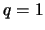 .
.
Suponhamos agora que 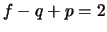 para grafos com mais que 1 face com
para grafos com mais que 1 face com 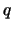 arestas. Seja
arestas. Seja 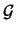 um grafo conexo com
um grafo conexo com 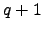 arestas e mais que uma face. Seja
arestas e mais que uma face. Seja 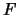 a face infinita. Existe então um ciclo
a face infinita. Existe então um ciclo 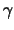 contido na fronteira de
contido na fronteira de 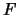 . Defina-se
. Defina-se
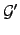 como o grafo obtido de
como o grafo obtido de 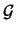 a que se retirou uma aresta
a que se retirou uma aresta 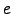 de
de 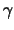 . Tem-se que, como
. Tem-se que, como 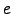 é aresta de um ciclo, o grafo
é aresta de um ciclo, o grafo
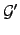 é conexo, planar e com
é conexo, planar e com 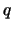 arestas. Sejam
arestas. Sejam 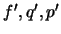 o número de faces, arestas e vértices, respectivamente, de
o número de faces, arestas e vértices, respectivamente, de
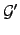 . As igualdade seguintes são válidas:
. As igualdade seguintes são válidas:
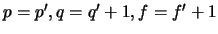 . Se
. Se 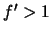 , então pela hipótese de indução
, então pela hipótese de indução
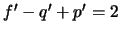 , e logo
, e logo 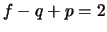 . Se
. Se 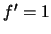 então
então
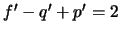 pelo que foi visto no início da demonstração, o que implica que
pelo que foi visto no início da demonstração, o que implica que 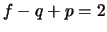 .
.
Vejamos um exemplo:
O grafo planar acima apresentado tem 3 faces, mas apenas uma delas tem um ciclo como fronteira.
Vejamos algumas consequências da fórmula de Euler:
Corolário 6.2
Dado um
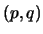
-grafo planar conexo com
faces tal que cada uma tem como fronteira um ciclo de comprimento
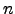
, então
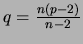
.
Visto cada face ter 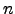 arestas e cada aresta está em fronteiras de 2 faces distintas, segue que
arestas e cada aresta está em fronteiras de 2 faces distintas, segue que 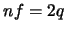 . Sendo
. Sendo 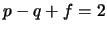 , então
, então
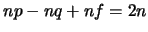 . Como
. Como 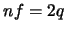 segue que
segue que
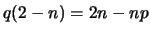 .
.
Um grafo planar diz-se maximal se não for possível acrescentar uma aresta (que não seja lacete) de forma a não se perder a planaridade do grafo.
Corolário 6.3
Se
é um grafo
planar maximal então a fronteira de cada face é
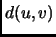
e
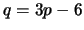
. Se
é um grafo
planar tal que a fronteira de cada face é
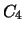
então
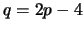
.
Basta substituir  por 3 e 4, respectivamente.
por 3 e 4, respectivamente.
Visto o número máximo de arestas ocorrer quando a fronteira de cada face é 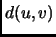 , são válidos os resultados seguintes:
, são válidos os resultados seguintes:
Corolário 6.4
Dado
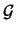
um grafo
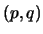
planar, com
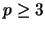
, então
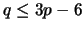
. Se
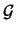
não tem subgrafos do tipo
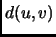
então
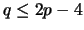
.
Corolário 6.5
Os grafos
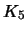
e
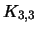
não são planares.
Para 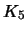 ,
,
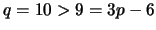 , e para
, e para  ,
,
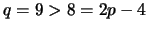 .
.
Um exemplo de cada um destes conceitos é, respectivamente,
Definição 6.7
Dois grafos
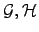
são homeomorfos se uma subdivisão de
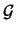
for isomorfa a uma subdivisão de
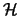
.
Os grafos seguintes são homeomorfos mas não são isomorfos:
Recordamos, então, o enunciado do Teorema de Kuratowski:
Teorema 6.8 (Teorema de Kuratowski)
Um grafo é planar se e só se não tem nenhum subgrafo homeomorfo a
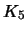
ou
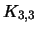
.
Uma contracção elementar do grafo 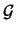 consiste na substituição de dois vértices
consiste na substituição de dois vértices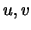 adjacentes por um novo vértice
adjacentes por um novo vértice 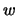 , acrescentando-se arestas de tal forma que
, acrescentando-se arestas de tal forma que 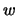 seja vizinho de todos os vizinhos de
seja vizinho de todos os vizinhos de 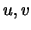 .
.
Por exemplo, considere o grafo
Vamos remover os vértices 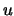 e
e 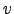 , assim como as arestas adjacentes a eles, acrescentando um vértice
, assim como as arestas adjacentes a eles, acrescentando um vértice 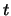 bem como arestas de forma a que
bem como arestas de forma a que 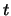 seja vizinho dos vértices que o eram de
seja vizinho dos vértices que o eram de 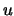 ou de
ou de 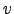 :
:
Um grafo 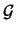 diz-se contractível num grafo
diz-se contractível num grafo 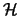 se
se 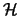 puder ser obtido de
puder ser obtido de 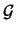 por contracções elementares. Por exemplo, o grafo apresentado atrás é contractível em
por contracções elementares. Por exemplo, o grafo apresentado atrás é contractível em 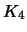 .
.
O resultado seguinte dá-nos outra forma de caracterizar os grafos planares:
Teorema 6.9 (Teorema de Wagner-Harary-Tutte)
Um grafo é planar se e só se não tiver um subgrafo contractível em
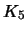
ou
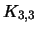
.




Seguinte: Grafos eulerianos e grafos
Acima: Breve introdução à teoria
Anterior: Caminhos e conexidade
Conteúdo
Pedro Patricio
2006-05-29
![$\displaystyle \xymatrix{
1 \ar@{-}[rrr]\ar@{-}[rd] & & &2 \ar@{-}[ld] \ar@{-}[d...
... 8 \ar@{-}[r] \ar@{-}[ld] & 7 &\\
4 \ar@{-}[rrr]\ar@{-}[uuu]& & &3\ar@{-}[lu]}$](img328.png)
![$\displaystyle \xymatrix{
1 \ar@{-}[rrr]\ar@{-}[rd] & & &2 \ar@{-}[ld] \ar@{-}[d...
... 8 \ar@{-}[r] \ar@{-}[ld] & 7 &\\
4 \ar@{-}[rrr]\ar@{-}[uuu]& & &3\ar@{-}[lu]}$](img328.png)
![]() ou
ou ![]() .
.
![]() , é o conjunto das arestas que delimitam a face
, é o conjunto das arestas que delimitam a face ![]() , ou que estão contidas em
, ou que estão contidas em ![]() .
.
![]() ; a igualdade é provada por indução sobre o número de arestas.
; a igualdade é provada por indução sobre o número de arestas.
![]() então
então ![]() e
e ![]() , ou então
, ou então ![]() , e portanto
, e portanto ![]() . Uma representação destes dois casos é, respectivamente,
. Uma representação destes dois casos é, respectivamente,
![$\displaystyle \xymatrix{
\bullet \ar@{-}[r]& \bullet}\hspace*{2cm} \xymatrix{ \bullet \ar@(ul,ur)}$](img342.png)
![$\displaystyle \xymatrix{\bullet \ar@{-}[rrr]\ar@{-}[rrrdd]^{F_2}\ar@{-}[dd] & &...
...et\\
&\bullet\ar@{-}[ld]_{F_1} & & & \\
\bullet\ar@{-}[rrr] & & & \bullet & }$](img349.png)
![]() , são válidos os resultados seguintes:
, são válidos os resultados seguintes:
![$\displaystyle \xymatrix{\bullet \ar@{-}[rd] & & &\\
\circ \ar@{-}[u]\ar@{-}[d]...
...et \ar@{-}[r] &\circ\ar@{-}[r]& \bullet \\
\bullet\ar@{-}[uu] \ar@{-}[ru] &&&}$](img372.png)
![]() consiste na substituição de dois vértices
consiste na substituição de dois vértices![]() adjacentes por um novo vértice
adjacentes por um novo vértice ![]() , acrescentando-se arestas de tal forma que
, acrescentando-se arestas de tal forma que ![]() seja vizinho de todos os vizinhos de
seja vizinho de todos os vizinhos de ![]() .
.
![$\displaystyle \xymatrix{
& u \ar@{-}[ld] \ar@{-}[ldd]\ar@{-}[rdd] \ar@{-}[rd] & \\
y \ar@{-}[d] \ar@{-}[rrd] && v\ar@{-}[d]\ar@{-}[lld]\\
x \ar@{-}[rr] && w}$](img132.png)
![$\displaystyle \xymatrix{
y\ar@{-}[r]\ar@{-}[rd]\ar@{-}[d] & t\ar@{-}[d] \\
x\ar@{-}[r]\ar@{-}[ru] & w}$](img375.png)
![]() diz-se contractível num grafo
diz-se contractível num grafo ![]() se
se ![]() puder ser obtido de
puder ser obtido de ![]() por contracções elementares. Por exemplo, o grafo apresentado atrás é contractível em
por contracções elementares. Por exemplo, o grafo apresentado atrás é contractível em ![]() .
.