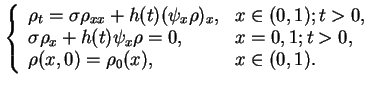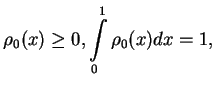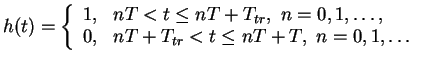Mouse over the titles shows the abstracts.   A pdf version of the schedule is available here.

  14:00 - 14:30   Registration

  14:30 - 15:15   Neville Ford

   Fractional differential equations: numerical methods for initial and boundary value problems

In this talk we begin with a survey to introduce the basic ideas of the fractional calculus. We focus on fractional differential equations of Caputo type and we explore how they may be solved numerically. We give examples that show why numerical methods must be chosen very carefully for initial value problems and we explain why simple approaches often lead to unsatisfactory results. We move on to consider boundary value problems and we provide some new theoretical results that underpin the analysis. Finally we give examples of suitable numerical methods for boudary value fractional differential equations.

  15:15 - 16:00   Pedro Lima

   Differential equations with bubble-type solutions: analysis and numerical simulations

This talk is devoted to singular boundary value problems arising in hydrodynamics and cosmology. In the case of spherical simmetry, the original partial differential equation may be reduced to a second order nonlinear ordinary differential equation (ODE). This is the case, for example, of the formation of bubbles or droplets in a mixture gas-liquid. We are interested on solutions of the resulting ODE which are strictly increasing on the positive semi-axis and have finite limits at 0 and ∞ (bubble-type solutions). Necessary and sufficient conditions for the existence of such solutions are obtained in the form of a restriction on the equation coefficients. The asymptotic behavior of certain solutions of this equation is analysed near the two singularities (when r → 0⁺ and r → ∞), where the considered boundary conditions define one-parameter families of solutions. Based on the analytic study, efficient numerical methods are proposed to compute approximately the needed solutions of the above problem. Some results of the numerical experiments are displayed and their physical interpretation is discussed.

  16:00 - 16:20   Carla Pinto

   ODEs and CPGs models for locomotion

In this talk we will review the application of networks of cells/neurons to model locomotion patterns in animals. Each cell/neuron is modeled by a system of ordinary differential equations. This study has been lately applied in robotics, in the generation of trahectories of robots with two, three or more legs.

coffee break

  16:50 - 17:35   Pedro Girão

    Bifurcation curves of a diffusive logistic equation with harvesting

We construct the global bifurcation curves for the steady states of a diffusive logistic equation with harvesting on a bounded domain, under Dirichlet boundary conditions and other appropriate hypotheses, when the linear growth rate of the population is below λ₂+δ. Our analysis provides new information on the number of solutions.

  17:35 - 17:55   Fernando Carapau

   Average pressure gradient of swirling flow motion of a viscoelastic fluid in a circular straight tube with no constant radius

Motived by the aim of modelling the behavior of swirling flow motion, we present a 1D hierarchical model for an Rivlin-Ericksen fluid with complexity n=2 flowing in a circular straight tube with no constant radius. Integrating the equation of conservation of linear momentum over the tube cross-section, with t he velocity field approximated by the Cosserat theory, we obtain a one-dimension al system depending only on time and on a single spatial variable. The velocity field approximation satisfies both the incompressibility condition and the kinem atic boundary condition exactly. From this new system, we derive the equation fo r the wall shear stress and the relationship between average pressure gradient, volume flow rate and swirling scalar function over a finite section of the tube. Also, we obtain the corresponding partial differential equation for the swirlin g scalar function.

  17:55 - 18:15   José Joaquim Oliveira

   General criterion for exponential stability of neural network models with unbounded distributed delays

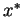
In this talk, we establish sufficient conditions for the existence and global exponential stability of an equilibrium point of the following general neural network model with infinity distributed delays We apply the general result to several delayed neural networks models, such as Cohen-Grossberg neural networks, bidirectional associative memory neural networks, and cellular neural networks with S-type distributed delays, generalizing known results in the literature.
We emphasize that, contrary to the usual, we do not use Lyapunov functionals to obtain our results, which can therefore be applied to a very general setting.
Joint work with Teresa Faria (CMAF, Univ. Lisboa).

meeting dinner

    9:30 - 10:15   Adélia Sequeira

    3D FSI modeling and simulations of blood flow in the vascular system

Blood flow interacts mechanically with the vessel wall, giving rise to pressure waves propagating in arteries, which deform under the action of blood pressure. In order to capture these phenomena, complex fluid-structure interaction (FSI) problems must be considered, coupling physiologically meaningful models for both the blood and the vessel wall. From the theoretical point of view, this is extremely difficult because of the high non-linearity of the problem and the low regularity of the displacement of the fluid-structure interface. So far, mathematical results have been obtained only in simplified cases. From the numerical point of view, the use of partitioned schemes which solve iteratively the fluid and the structure sub-problems, supplied with suitable transmission conditions, is difficult to handle in hemodynamic problems, due to the large added mass effect.
In this talk we introduce some recent mathematical models of the cardiovascular system and comment on their significance to yield realistic and accurate numerical results. Simulations of the mechanical interaction between blood flow and vessel walls will be shown. A 3D FSI model in a compliant vessel is used to describe the pressure wave propagation. The 3D fluid is described through a shear-thinning generalized Newtonian model and the structure by a hyperelastic model. In order to cope with the spurious reflections due to the truncation of the computational domain, several absorbing boundary conditions are analyzed. Firstly, a 1D hyperbolic model that effectively captures the wave propagation nature of blood flow in arteries is coupled with the 3D FSI model. Moreover, absorbing boundary conditions obtained from the 1D model are imposed directly on the outflow sections of the 3D FSI model, and numerical results comparing the different absorbing conditions in an idealized vessel are presented. Results in a realistic carotid bifurcation are also provided in order to show that the proposed methodology can be applied to physiological geometries.

  10:15 - 11:00   M. Carmen Muñiz

    Some PDE problems with industrial applications

This talk summarizes several mathematical problems formulated in terms of partial differential equations with direct and challenging applications in industry, such as metal purification, process optimization and newly-designed flat-plate solar collectors.

coffee break

  11:30 - 11:50   Clara Carlota

   Recent applications of reparametrization and bimonotonicity techniques to the calculus of variations

We review recent applications of reparametrization and bimonotonicity techniques to obtain sufficient and necessary conditions for existence of minimizers in the calculus of variations.
Joint work with A. Ornelas, Univ. de Évora.

  11:50 - 12:35   José Francisco Rodrigues

   Constrained reaction-diffusion and transport systems: the N-membrane and multiphase problems

We analyse vector valued diffusion and transport equations with a class of constraints of unilateral and bilateral type. Using the variational inequality approach we characterize explicitly the associated Lagrange multipliers by reducing the problems to semi-linear systems coupled through the characteristic functions of the coincident sets of the N-membranes problem, analogously to the obstacle problem. In collaboration with Lisa Santos, we obtain new results to the system associated with the Gibbs simplex for multiphase problems. We also discuss the stability of the solutions and their coincident sets, in particular, the asymptotic behaviour in time for the respective evolution problems.

lunch

  14:30 - 15:15   Dmitry Vorotnikov

    The flashing ratchet and unidirectional transport

Nano-scale or molecular devices which use energy but not momentum to generate transport are called Brownian motors. Such phenomena arise in different areas of science, from intracellular transport to nanotechnology. We consider the flashing ratchet model of a Brownian motor which is described by the IBVP

Here the density 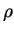is unknown, 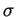is the diffusion coefficient,

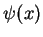
and is the asymmetric ratchet-like potential.
We prove that such a model with proper parameters really leads to unidirectional transport of matter.

  15:15 - 16:00   Fábio Chalub

   Discrete and continuous models in population dynamics

We consider in this talks an hierarchy of models, starting from discrete models for population dynamics and ending in ordinary differential equations. We will be forced to introduced partial differential equations of singular type as an intermediate models linking the discrete and the ODE model. This model will be an approximation of the discrete model for all time scales, and will be approximated by the ODE model for short times. Uniqueness of solution will be guaranteed by conservation laws, and not by boundary conditions.

  16:00 - 16:20   Paulo Amorim

   Numerical schemes for short wave long wave interaction equations

We present some convergence results for numerical approximations of a system of PDEs modeling short wave long wave interactions. These consist of a nonlinear Schroedinger equation coupled with either a nonlinear conservation law or a KdV equation. Numerical examples are presented, shedding light on some open problems.
This is joint work with M. Figueira of CMAF.

coffee break

  16:50 - 17:35   Pedro Freitas

   PDEs, computers and applications

We discuss the interplay between the usage of computer simulations and manipulations and more classical analysis in the field of partial differential equations and its applications. By considering examples taken from the spectral theory of the Laplacian, we shall illustrate possible ways in which the two approaches complement each other and how to take advantage of both.

  17:35 - 18:15   poster session

                                    Joaquim Pinho da Cruz

FEM and XFEM: theoretical and implementation aspects, and applications in solid mechanics
Abstract:  The finite element method (FEM) is one of the most efficient tools used for the numerical solution of partial differential equations in computational solid mechanics. On the other hand, in FEM modelling of evolving discontinuities, such as cracks, finite element mesh must conform the geometry of the crack, and there is the need to remesh, i.e., to use adaptive mesh refinement, which leads to cumbersome mesh processes, computational cost and loss of accuracy due data mapping form old to new meshes. In this context, the extended finite element method (XFEM) is a FEM generalisation that enables the incorporation of local enrichment of approximation spaces. So, XFEM enables the generation of a FEM mesh without discontinuities (e.g. cracks), followed by the enrichment of the FEM approximation with functions that model those discontinuities, leading to simpler numerical modelling of complex processes. The main aspects of both FEM and XFEM methods are reviewed, and some general aspects related to their numerical implementation and examples of their application on solid mechanics are presented.
Joint work with J.A. Oliveira (Univ.Aveiro).

                                    Raquel Barreira

Surface Finite Element Method for Pattern Formation on Growing Biological Surfaces
Abstract:  We propose models based on reaction diffusion systems and numerical methods to reproduce pattern formation on growing surfaces. The numerical method is based on the Surface Finite Element Method introduced by Dziuk and Elliott [1]. The key idea is based on the approximation of the surface by a triangulated one consisting of a union of triangles with vertices on the original surface which allows us to simulate pattern formation on the skin of a growing organism by approximating its shape by a triangulation. Another application we propose is the growth of solid tumours for which the surface of the tumour deforms according to the concentration of a chemi cal that promotes growth.

---

[1]Dziuk, G. and Elliott, C. M. Surface finite elements for parabolic equations. J. Comp. Math.,25:430-439,2007

                                    Sílvia Chá

Recent applications of reparametrization and bimonotonicity techniques to optimal control
Abstract:  We review recent applications of reparametrization and bimonotonicity for existence of optimal solutions in optimal control.
Joint work with A. Ornelas and C. Carlota.

dinner

    9:30 - 10:15   Chérif Amrouche

   L^p-theory for vector potentials and elliptical systems with non standard boundary conditions

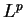
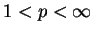
We consider here elliptical systems as Stokes problems in a bounded domain, eventually multiply connected, whose boundary consists of multi-connected components. We investigate the solvability in theory, with , under the non standard boundary conditions The main ingredients for this solvability are given by the Inf-Sup conditions, some Sobolev's inequalities for vector fields and the theory of vector potentials satisfying Those inequalities play a fundamental key and are obtained thanks to Calderon-Zygmund inequalities and integral representations. In the study of elliptical problems, we consider both generalized solutions and strong solutions that very weak solutions. Finally, this work is an extension of [1] where the authors give the hilbertian theory for vector potentials.

---

[1] C. Amrouche, C. Bernardi, M. Dauge and V. Girault, Vector Potentials In Threedimensional Non-smooth Domains, Math. Meth. Applied Sc., Vol. 21, pp. 823-864, 1998.

  10:15 - 11:00   Ana Jacinta Soares

   Mathematical problems of multicomponent reactive flows

Multicomponent reactive flows have been extensively investigated since the middle of the past century due to their central role in a wide range of practical applications, such as combustion engineering, plasma physics, chemical reactors and many other industrial processes. In particular, many contributions have been proposed within the kinetic theory of reactive mixtures concerning for example the modeling of multicomponent flows, consistency of macroscopic theories in the hydrodynamic limit, evaluation of transport coefficients as well as existence theory, stability and long-time behavior of solutions.
In this talk, some recent studies arising in the kinetic theory of reactive mixtures will be presented, mainly addressed to the modeling of multicomponent reactive flows, mathematical structure and properties of the governing equations and existence, uniqueness, and stability results.

coffee break

  11:30 - 11:50  Hugo Tavares

   Asymptotic study of nonlinear Schroedinger systems with strong competition

We consider a class of nonlinear Schroedinger systems with competition terms arising in the theory of Bose-Einstein condensation. For such systems, we study the asymptotics of its solutions as the competition term go to infinity, proving convergence. The limiting profiles are Lipschitz continuous and segregated, and we st udy the regularity properties of their nodal sets. We present a general regularity theory which can be applied to other free boundary problems.

  11:50 - 12:35   Vincenzo Vespri

   Harnack inequalities for degenerate parabolic equation

We consider nonnegative solution of degenerate parabolic equation whose protype is the p-Laplacean equation (p> 1). By using recent result we show how the classical Moser's results can be extended to the degenerate case (p>2), supercritical case (^2N⁄_N+1 < p < 2) and subcritical case (1 < p ≤ ^2N⁄_N+1)

lunch

  14:00   Douro River cruise [optional]