



Seguinte: Produto
Acima: Operações matriciais
Anterior: Operações matriciais
Conteúdo
Sejam
![$ A=\left[a_{ij} \right], B=\left[b_{ij} \right]\in \mathcal{M}_{m\times n}\left( {\mathbb{K}}\right)$](img65.png) e
e
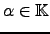 .
.
- A soma entre matrizes
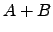 é a matriz
é a matriz
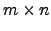 cujo elemento
cujo elemento 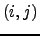 é
é
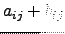 . Ou seja,
. Ou seja,
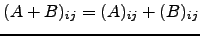 .
.
- O produto de uma matriz com um escalar
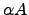 é a matriz
é a matriz
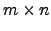 cujo elemento
cujo elemento 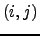 é
é
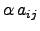 . Ou seja,
. Ou seja,
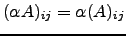 .
.
Repare que a soma de duas matrizes, da mesma ordem, é feita elemento a elemento, e o produto escalar de uma matriz por
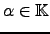 é de novo uma matriz da mesma ordem da dada, onde cada entrada surge multiplicada por
é de novo uma matriz da mesma ordem da dada, onde cada entrada surge multiplicada por 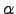 . Ou seja,
. Ou seja,
e
Por exemplo,
e
Como é fácil de compreender, a soma e o produto escalar são comutativos.
De ora em diante, 0 representa uma qualquer matriz cujos elementos são nulos, e se
![$ A= \left[a_{ij} \right]$](img54.png) então
então
![$ -A=\left[-a_{ij}\right]$](img78.png) .
.
Estas operações satisfazem as propriedades que de seguida se descrevem, onde
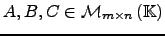 e
e
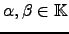 :
:
- A soma de matrizes é associativa:
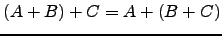 .
.
- A soma de matrizes é comutativa:
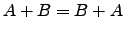
- A matriz nula é o elemento neutro da adição:
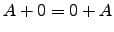 .
.
- Existe o simétrico de cada matriz
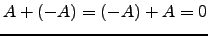 .
.
-
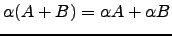 .
.
-
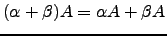 .
.
-
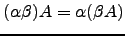 .
.
-
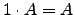 .
.




Seguinte: Produto
Acima: Operações matriciais
Anterior: Operações matriciais
Conteúdo
Pedro Patricio
2008-01-08
![]() e
e
![]() .
.
![]() é de novo uma matriz da mesma ordem da dada, onde cada entrada surge multiplicada por
é de novo uma matriz da mesma ordem da dada, onde cada entrada surge multiplicada por ![]() . Ou seja,
. Ou seja,
![$\displaystyle \left[\begin{array}{cccc}
a_{11}&a_{12}&\dots &a_{1m}\\
a_{21}&a...
...& \vdots \\
a_{n1}+b_{n1}&a_{n2}+b_{n2}&\dots &a_{nm}+b_{nm}\end{array}\right]$](img74.png)
![$\displaystyle \alpha \left[\begin{array}{cccc}
a_{11}&a_{12}&\dots &a_{1m}\\
a...
... \vdots \\
\alpha a_{n1}&\alpha a_{n2}&\dots &\alpha a_{nm}\end{array}\right].$](img75.png)
![$\displaystyle \left[\begin{array}{cc}1&2 3&4\end{array}\right]+ \left[\begin{...
...\end{array}\right]=
\left[\begin{array}{cc}1+5&2+6 3+7& 4+8\end{array}\right]$](img76.png)
![$\displaystyle 5\left[\begin{array}{cc}1&2 3&4\end{array}\right]=\left[\begin{array}{cc}5 \cdot 1&5 \cdot 2 5 \cdot 3&5 \cdot 4\end{array}\right].$](img77.png)
![]() então
então
![]() .
.
![]() e
e
![]() :
: