



Seguinte: Propriedades das transformações lineares
Acima: Transformações lineares
Anterior: Transformações lineares
Conteúdo
Definição 6.1.1
Sejam 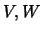 espaços vectoriais sobre
espaços vectoriais sobre
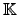 . Uma transformação linear ou aplicação linear de
. Uma transformação linear ou aplicação linear de 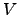 em
em 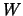 é uma função
é uma função
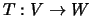 que satisfaz, para
que satisfaz, para
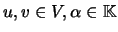 ,
,
-
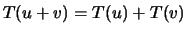 ;
;
-
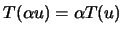 .
.
Para
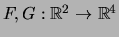 definidas por
definidas por
e
tem-se que 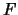 é linear enquanto
é linear enquanto 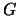 não o é. De facto, para
não o é. De facto, para
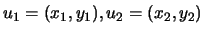 e
e
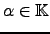 , temos
, temos
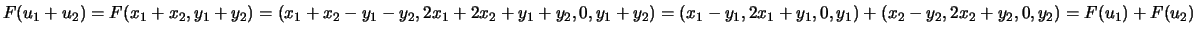 , e
, e
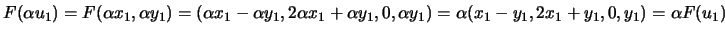 , enquanto que
, enquanto que
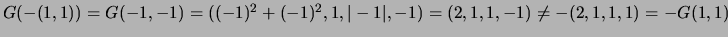
Apresentamos alguns exemplos clássicos de transformações lineares:
- Sejam
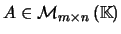 e
e
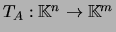 definida por
definida por 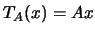 . A aplicação
. A aplicação 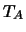 é uma transformação linear. Ou seja, dada uma matriz, existe uma transformação linear associada a ela. No entanto, formalmente são entidades distintas. Mais adiante, iremos ver que qualquer transformação linear está associada a uma matriz.
é uma transformação linear. Ou seja, dada uma matriz, existe uma transformação linear associada a ela. No entanto, formalmente são entidades distintas. Mais adiante, iremos ver que qualquer transformação linear está associada a uma matriz.
- Seja
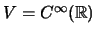 o espaço vectorial sobre
o espaço vectorial sobre
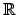 constituído pelas funções reais de variável real infinitamente (continuamente) diferenciáveis sobre
constituído pelas funções reais de variável real infinitamente (continuamente) diferenciáveis sobre
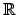 . Seja
. Seja
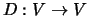 definida por
definida por 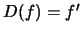 . Então, usando noções elementares de análise, é uma transformação linear.
. Então, usando noções elementares de análise, é uma transformação linear.
- A aplicação
![$ F:{\mathbb{K}}_n[x] \rightarrow {\mathbb{K}}_{n-1}[x]$](img1327.png) definida por
definida por 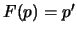 , onde
, onde
![$ p \in {\mathbb{K}}_ n[x]$](img1329.png) e
e 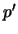 denota a derivada de
denota a derivada de 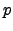 em ordem a
em ordem a 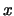 , é uma transformação linear.
, é uma transformação linear.
- Sejam
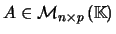 e
e
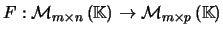 definida por
definida por 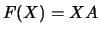 . Usando as propriedades do produto matricial,
. Usando as propriedades do produto matricial, 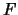 é uma transformação linear.
é uma transformação linear.
- A aplicação
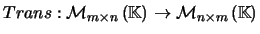 definida por
definida por
 é uma transformação linear.
é uma transformação linear.
- Seja
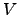 um espaço vectorial arbitrário sobre
um espaço vectorial arbitrário sobre
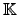 . As aplicações
. As aplicações
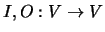 definidas por
definidas por 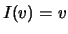 e
e 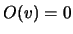 são transformações lineares. Denominam-se, respectivamente, por transformação identidade e transformação nula.
são transformações lineares. Denominam-se, respectivamente, por transformação identidade e transformação nula.




Seguinte: Propriedades das transformações lineares
Acima: Transformações lineares
Anterior: Transformações lineares
Conteúdo
Pedro Patricio
2008-01-08
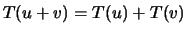 ;
;
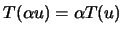 .
.
![]() definidas por
definidas por