


Seguinte: Sobre este documento ...
Universidade do Minho
MiEB
Departamento de Matemática
Álgebra Linear C
folha vii
2007/2008
- Considere a matriz
![$ A=\left[\begin{array}{ccc} 2 & 0 & 0\\
-8 &4 &-6\\
8 &1 &9\end{array}\right]$](img1.png) .
.
- Calcule o polinómio característico de
 .
.
- Use o comando poly(A) para confirmar o resultado que obteve na alínea anterior.
- Calcule os valores próprios de
 .
.
- Confirme os resultados obtidos na alínea anterior usando o comando [v,e] = eig(A).
- Compare o determinante de
 com o produto dos seus valores próprios.
com o produto dos seus valores próprios.
- Compare o traço1 de
 com a soma dos seus valores próprios.
com a soma dos seus valores próprios.
- Calcule os valores próprios de
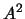 , fazendo
, fazendo > eig(A^2)
e compare-os com os quadrados dos valores próprios de  .
.
- Seja
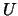 a matriz cujas colunas são os vectores próprios linearmente independentes. Por exemplo, pode tomar
a matriz cujas colunas são os vectores próprios linearmente independentes. Por exemplo, pode tomar 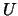 como a matriz v da alínea (d). Calcule
como a matriz v da alínea (d). Calcule 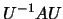 .
.
- Troque duas colunas da matriz
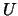 descrita na alínea anterior e efectue, de novo, o produto
descrita na alínea anterior e efectue, de novo, o produto 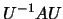 . Comente o resultado obtido.
. Comente o resultado obtido.
- Considere a matriz B = [1,-1; 1,1].
- Calcule o polinómio característico e mostre que
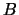 não tem valores próprios reais.
não tem valores próprios reais.
- Compare o determinante de
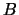 com o produto dos seus valores próprios.
com o produto dos seus valores próprios.
- Compare o traço de
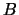 com a soma dos seus valores próprios.
com a soma dos seus valores próprios.
- Calcule os valores próprios de
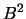 compare-os com os quadrados dos valores próprios de
compare-os com os quadrados dos valores próprios de 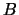 .
.
- Seja
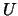 a matriz cujas colunas são os vectores próprios linearmente independentes. Calcule
a matriz cujas colunas são os vectores próprios linearmente independentes. Calcule 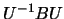 .
.
- Troque duas colunas da matriz
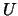 descrita na alínea anterior e efectue, de
novo, o produto
descrita na alínea anterior e efectue, de
novo, o produto 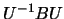 . Comente o resultado obtido.
. Comente o resultado obtido.
- Considere a matriz C=[2 1 0; 0 2 0; 0 0 3].
- Calcule o polinómio característico e os valores próprios (e a sua multiplicidade algébrica).
- Calcule a dimensão dos respectivos espaços próprios.
- Compare as multiplicidades algébrica e geométrica.
- Mostre que a matriz não é diagonalizável.
- Mostre que
- se
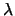 é valor próprio de
é valor próprio de  então
então 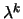 é valor próprio de
é valor próprio de 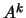 ;
;
- uma matriz nilpotente não tem valores próprios não nulos.
- Mostre que duas matrizes semelhantes têm o mesmo espectro.
- Para cada uma das seguintes matrizes, calcule os valores próprios e os respectivos espaços próprios (indicando uma base para os espaços próprios).
(a)
![$ \left[\begin{array}{cc}
4 & -5\\ 2 & -3 \end{array}\right]$](img12.png) |
(b)
![$ \left[\begin{array}{cc}
2 & 1\\ -1 & 0 \end{array}\right]$](img13.png) |
(c)
![$ \left[\begin{array}{cc}
0 & 1\\ -1 & 0 \end{array}\right]$](img14.png) |
(d)
![$ \left[\begin{array}{cc}
1 & 1\\ 0 & 1 \end{array}\right]$](img15.png) |
(e)
![$ \left[\begin{array}{ccc}
1 & -1 & 0\\ -1 & 2 & -1\\ 0 & -1 & 1\end{array}\right]$](img16.png) |
(f)
![$ \left[\begin{array}{ccc}
3 & 2 & 4\\ 2 & 0 & 2\\ 4 & 2 & 3\end{array}\right]$](img17.png) |
(g)
![$ \left[\begin{array}{ccc}
-3 & 1 & -1\\ -7 & 5 & -1\\ -6 & 6 & -2\end{array}\right]$](img18.png) |
(h)
![$ \left[\begin{array}{ccc}
2 & 1 & 1\\ 2 & 3 & 2\\ 3 & 3 & 4\end{array}\right]$](img19.png) |
|
- Calcule
![$ \left[\begin{array}{cc} 3 & 4\\ 5 & 2 \end{array}\right]^9$](img20.png) .
.
- Considere a matriz
![$ A=\left[\begin{array}{ccc}
8&1&3\\ 0 & -3 & -6\\ 0 & 1 & 2 \end{array}\right]$](img21.png) .
.
- Determine os valores próprios de
 .
.
- Determine os vectores próprios de
 e diagonalize
e diagonalize  .
.
- Usando o resultado da alínea
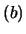 , determine uma matriz
, determine uma matriz 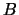 tal que
tal que 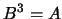 .
.
- Considere a matriz
![$ A=\left[\begin{array}{cc} 2&3\\ 3&2 \end{array}\right]$](img24.png) .
.
- Verifique que
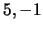 são os valores próprios de
são os valores próprios de  .
.
- Verifique se
![$ \left[\begin{array}{c} -1\\ 1\end{array}\right]$](img26.png) é vector próprio associado ao valor próprio
é vector próprio associado ao valor próprio 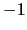 e se
e se
![$ \left[\begin{array}{c} 1\\ 1\end{array}\right]$](img28.png) é vector próprio associado ao valor próprio 5.
é vector próprio associado ao valor próprio 5.
- Diga, justificando, se a matriz
![$ \left[\begin{array}{cc} -1&1\\ 1&1\end{array}\right]$](img29.png) é invertível, e caso afirmativo calcule a sua inversa.
é invertível, e caso afirmativo calcule a sua inversa.
- Diga, justificando, se a matriz
 é diagonalizável, e caso
afirmativo, diagonalize-a.
é diagonalizável, e caso
afirmativo, diagonalize-a.
- Considere a matriz
![$ A=\left[\begin{array}{cc} 1&2\\ 2&1 \end{array}\right]$](img30.png) .
.
- Verifique que
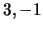 são os valores próprios de
são os valores próprios de  .
.
- Verifique se
![$ \left[\begin{array}{c} 1\\ 1\end{array}\right]$](img28.png) é vector próprio associado ao valor próprio 3 e se
é vector próprio associado ao valor próprio 3 e se
![$ \left[\begin{array}{c} -1\\ 1\end{array}\right]$](img26.png) é vector próprio associado ao valor próprio -1.
é vector próprio associado ao valor próprio -1.
- Diga, justificando, se a matriz
![$ \left[\begin{array}{cc} 1&-1\\ 1&1\end{array}\right]$](img32.png) é invertível, e caso afirmativo calcule a sua inversa.
é invertível, e caso afirmativo calcule a sua inversa.
- Diga, justificando, se a matriz
 é diagonalizável, e caso afirmativo, diagonalize-a.
é diagonalizável, e caso afirmativo, diagonalize-a.
- Considere a matriz
![$ A=\left[\begin{array}{cc} 2&-2\\ 2&-3 \end{array}\right]$](img33.png) .
.
- Verifique que
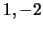 são os valores próprios de
são os valores próprios de  .
.
- Verifique se
![$ \left[\begin{array}{c} 2\\ 1\end{array}\right]$](img35.png) é vector próprio associado ao valor próprio
é vector próprio associado ao valor próprio 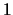 e se
e se
![$ \left[\begin{array}{c} 1\\ 2\end{array}\right]$](img37.png) é vector próprio associado ao valor próprio
é vector próprio associado ao valor próprio 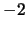 .
.
- Diga, justificando, se a matriz
![$ \left[\begin{array}{cc} 2&1\\ 1&2\end{array}\right]$](img39.png) é invertível, e caso afirmativo calcule a sua inversa.
é invertível, e caso afirmativo calcule a sua inversa.
- Diga, justificando, se a matriz
 é diagonalizável, e caso afirmativo, diagonalize-a.
é diagonalizável, e caso afirmativo, diagonalize-a.
- Considere a matriz
![$ A=\left[\begin{array}{cc} 1&2\\ 2&-2 \end{array}\right]$](img40.png) .
.
- Verifique que
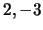 são os valores próprios de
são os valores próprios de  .
.
- Verifique se
![$ \left[\begin{array}{c} -1\\ 2\end{array}\right]$](img42.png) é vector próprio associado ao valor próprio
é vector próprio associado ao valor próprio 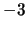 e se
e se
![$ \left[\begin{array}{c} 2\\ 1\end{array}\right]$](img35.png) é vector próprio associado ao valor próprio 2.
é vector próprio associado ao valor próprio 2.
- Diga, justificando, se a matriz
![$ \left[\begin{array}{cc} -1&2\\ 2&1\end{array}\right]$](img44.png) é invertível, e caso afirmativo calcule a sua inversa.
é invertível, e caso afirmativo calcule a sua inversa.
- Diga, justificando, se a matriz
 é diagonalizável, e caso
afirmativo, diagonalize-a.
é diagonalizável, e caso
afirmativo, diagonalize-a.
- Dada a matriz real
![$ A=\left[\begin{array}{cc} 1&0 \\ 1 &1\end{array}\right]$](img45.png) ,
,
- calcule os valores próprios e respectivos espaços próprios;
- verifique que a matriz dada não é
diagonalizável.



Seguinte: Sobre este documento ...
Pedro Patricio
2008-01-07
![$ A=\left[\begin{array}{ccc} 2 & 0 & 0\\
-8 &4 &-6\\
8 &1 &9\end{array}\right]$](img1.png) .
.
 .
.
 .
.
 com o produto dos seus valores próprios.
com o produto dos seus valores próprios.
 com a soma dos seus valores próprios.
com a soma dos seus valores próprios.
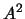 , fazendo
, fazendo  .
.
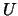 a matriz cujas colunas são os vectores próprios linearmente independentes. Por exemplo, pode tomar
a matriz cujas colunas são os vectores próprios linearmente independentes. Por exemplo, pode tomar 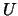 como a matriz v da alínea (d). Calcule
como a matriz v da alínea (d). Calcule 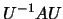 .
.
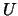 descrita na alínea anterior e efectue, de novo, o produto
descrita na alínea anterior e efectue, de novo, o produto 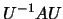 . Comente o resultado obtido.
. Comente o resultado obtido.
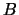 não tem valores próprios reais.
não tem valores próprios reais.
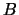 com o produto dos seus valores próprios.
com o produto dos seus valores próprios.
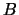 com a soma dos seus valores próprios.
com a soma dos seus valores próprios.
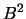 compare-os com os quadrados dos valores próprios de
compare-os com os quadrados dos valores próprios de 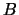 .
.
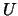 a matriz cujas colunas são os vectores próprios linearmente independentes. Calcule
a matriz cujas colunas são os vectores próprios linearmente independentes. Calcule 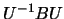 .
.
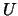 descrita na alínea anterior e efectue, de
novo, o produto
descrita na alínea anterior e efectue, de
novo, o produto 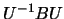 . Comente o resultado obtido.
. Comente o resultado obtido.
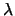 é valor próprio de
é valor próprio de  então
então 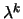 é valor próprio de
é valor próprio de 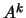 ;
;
![$ \left[\begin{array}{cc}
4 & -5\\ 2 & -3 \end{array}\right]$](img12.png)
![$ \left[\begin{array}{cc}
2 & 1\\ -1 & 0 \end{array}\right]$](img13.png)
![$ \left[\begin{array}{cc}
0 & 1\\ -1 & 0 \end{array}\right]$](img14.png)
![$ \left[\begin{array}{cc}
1 & 1\\ 0 & 1 \end{array}\right]$](img15.png)
![$ \left[\begin{array}{ccc}
1 & -1 & 0\\ -1 & 2 & -1\\ 0 & -1 & 1\end{array}\right]$](img16.png)
![$ \left[\begin{array}{ccc}
3 & 2 & 4\\ 2 & 0 & 2\\ 4 & 2 & 3\end{array}\right]$](img17.png)
![$ \left[\begin{array}{ccc}
-3 & 1 & -1\\ -7 & 5 & -1\\ -6 & 6 & -2\end{array}\right]$](img18.png)
![$ \left[\begin{array}{ccc}
2 & 1 & 1\\ 2 & 3 & 2\\ 3 & 3 & 4\end{array}\right]$](img19.png)
![$ \left[\begin{array}{cc} 3 & 4\\ 5 & 2 \end{array}\right]^9$](img20.png) .
.
![$ A=\left[\begin{array}{ccc}
8&1&3\\ 0 & -3 & -6\\ 0 & 1 & 2 \end{array}\right]$](img21.png) .
.
 .
.
 e diagonalize
e diagonalize  .
.
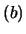 , determine uma matriz
, determine uma matriz 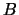 tal que
tal que 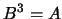 .
.
![$ A=\left[\begin{array}{cc} 2&3\\ 3&2 \end{array}\right]$](img24.png) .
.
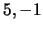 são os valores próprios de
são os valores próprios de  .
.
![$ \left[\begin{array}{c} -1\\ 1\end{array}\right]$](img26.png) é vector próprio associado ao valor próprio
é vector próprio associado ao valor próprio 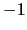 e se
e se
![$ \left[\begin{array}{c} 1\\ 1\end{array}\right]$](img28.png) é vector próprio associado ao valor próprio 5.
é vector próprio associado ao valor próprio 5.
![$ \left[\begin{array}{cc} -1&1\\ 1&1\end{array}\right]$](img29.png) é invertível, e caso afirmativo calcule a sua inversa.
é invertível, e caso afirmativo calcule a sua inversa.
 é diagonalizável, e caso
afirmativo, diagonalize-a.
é diagonalizável, e caso
afirmativo, diagonalize-a.
![$ A=\left[\begin{array}{cc} 1&2\\ 2&1 \end{array}\right]$](img30.png) .
.
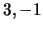 são os valores próprios de
são os valores próprios de  .
.
![$ \left[\begin{array}{c} 1\\ 1\end{array}\right]$](img28.png) é vector próprio associado ao valor próprio 3 e se
é vector próprio associado ao valor próprio 3 e se
![$ \left[\begin{array}{c} -1\\ 1\end{array}\right]$](img26.png) é vector próprio associado ao valor próprio -1.
é vector próprio associado ao valor próprio -1.
![$ \left[\begin{array}{cc} 1&-1\\ 1&1\end{array}\right]$](img32.png) é invertível, e caso afirmativo calcule a sua inversa.
é invertível, e caso afirmativo calcule a sua inversa.
 é diagonalizável, e caso afirmativo, diagonalize-a.
é diagonalizável, e caso afirmativo, diagonalize-a.
![$ A=\left[\begin{array}{cc} 2&-2\\ 2&-3 \end{array}\right]$](img33.png) .
.
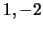 são os valores próprios de
são os valores próprios de  .
.
![$ \left[\begin{array}{c} 2\\ 1\end{array}\right]$](img35.png) é vector próprio associado ao valor próprio
é vector próprio associado ao valor próprio 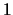 e se
e se
![$ \left[\begin{array}{c} 1\\ 2\end{array}\right]$](img37.png) é vector próprio associado ao valor próprio
é vector próprio associado ao valor próprio 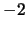 .
.
![$ \left[\begin{array}{cc} 2&1\\ 1&2\end{array}\right]$](img39.png) é invertível, e caso afirmativo calcule a sua inversa.
é invertível, e caso afirmativo calcule a sua inversa.
 é diagonalizável, e caso afirmativo, diagonalize-a.
é diagonalizável, e caso afirmativo, diagonalize-a.
![$ A=\left[\begin{array}{cc} 1&2\\ 2&-2 \end{array}\right]$](img40.png) .
.
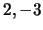 são os valores próprios de
são os valores próprios de  .
.
![$ \left[\begin{array}{c} -1\\ 2\end{array}\right]$](img42.png) é vector próprio associado ao valor próprio
é vector próprio associado ao valor próprio 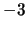 e se
e se
![$ \left[\begin{array}{c} 2\\ 1\end{array}\right]$](img35.png) é vector próprio associado ao valor próprio 2.
é vector próprio associado ao valor próprio 2.
![$ \left[\begin{array}{cc} -1&2\\ 2&1\end{array}\right]$](img44.png) é invertível, e caso afirmativo calcule a sua inversa.
é invertível, e caso afirmativo calcule a sua inversa.
 é diagonalizável, e caso
afirmativo, diagonalize-a.
é diagonalizável, e caso
afirmativo, diagonalize-a.
![$ A=\left[\begin{array}{cc} 1&0 \\ 1 &1\end{array}\right]$](img45.png) ,
,