Universidade do Minho
MiEB
Departamento de Matemática
Álgebra Linear C
folha iii
2007/2008
- Introduza a matriz A=[1,-3,1; 2,-4,2; 2,2,-3].
- Introduza os comandos
E1=eye(3)
E1(2,:)=-2*E1(1,:) + E1(2,:)
A1=E1*A
Explique como se obteve E1 à custa das linhas de 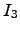 , e como se obteve A1 à custa das linhas de
, e como se obteve A1 à custa das linhas de 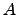 .
.
- Efectue os passos seguintes do Algoritmo de Eliminação de Gauss para obter a matriz escada
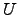 equivalente por linhas a
equivalente por linhas a 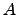 .
.
- Use as matrizes elementares de (a) para construir a matriz
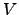 tal que
tal que 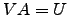 . Diga por que razão
. Diga por que razão 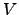 é invertível.
é invertível.
- Use a alínea anterior para determinar
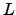 triangular inferior tal que
triangular inferior tal que 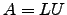 .
.
- Indique a característica da matriz
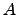 . Diga, justificando, se a matriz é invertível.
. Diga, justificando, se a matriz é invertível.
- Introduza a matriz B=[4,2,2,-2; 2,0,5,1; -2,-3,5,4].
- Efectue os passos do Algoritmo de Eliminação de Gauss para obter a matriz escada
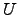 equivalente por linhas a
equivalente por linhas a 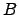 . Identifique os pivots.
. Identifique os pivots.
- Use as matrizes elementares de (a) para construir a matriz
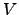 tal que
tal que 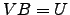 . Diga por que razão
. Diga por que razão 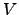 é invertível.
é invertível.
- Encontre a decomposição
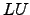 de
de 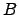 .
.
- Indique a característica da matriz
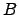 .
.
- Introduza a matriz C=[1,2,3; -2,-1,-5; -1,4,-3; 2,1,1].
- Efectue os passos do Algoritmo de Eliminação de Gauss para obter a matriz escada
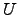 equivalente por linhas a
equivalente por linhas a 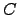 .
.
- Use as matrizes elementares de (a) para construir a matriz
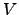 tal que
tal que 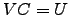 . Diga por que razão
. Diga por que razão 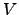 é invertível.
é invertível.
- Indique a característica da matriz
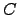 .
.
- Introduza a matriz G=[0,3,-2; -1,3,0; 2,3,-5].
- Efectue os passos do Algoritmo de Eliminação de Gauss para obter a matriz escada
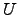 equivalente por linhas a
equivalente por linhas a 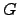 .
.
- Use as matrizes elementares de (a) para construir uma matriz
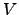 tal que
tal que 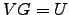 . Diga por que razão
. Diga por que razão 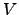 é invertível. Verifique se
é invertível. Verifique se 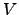 é triangular inferior.
é triangular inferior.
- Indique a característica da matriz
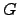 .
.
- Calcule a característica das matrizes seguintes, fazendo uso do Algoritmo de Eliminação de Gauss.
- Determine
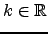 por forma que a característica da matriz
por forma que a característica da matriz
seja inferior a 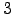 .
.
pedro
2007-11-06
![$\displaystyle \left[\begin{array}{ccc}6&3&-4\\ 1&2&5\\ 3&2&1 \end{array}\right]...
...&-3&2&2 \end{array}\right],
C=\left[\begin{array}{ccc}0&0&0 \end{array}\right],$](img17.png)
![$\displaystyle \left[\begin{array}{ccc} 4&3&1\\ 1&1&0\\ 2&3&1\\ 3&6&-2\end{array...
...[\begin{array}{ccc} 0&1&2\\ 1&2&3\\ 1&3&6\\ 2&6&11\\ 0&-1&-3\end{array}\right].$](img19.png)
![$\displaystyle F=\left[\begin{array}{cccc}
1&1&1&1\\
2&-1&2&1\\
1&2&1&k \end{array}\right]$](img21.png)