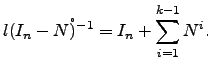- A matriz real
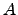 do tipo
do tipo 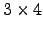 foi gerada aleatoriamente no Octave pela instrução
foi gerada aleatoriamente no Octave pela instrução
> A=fix(100*rand(3,4)-50);
Calcule 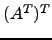 ,
, 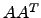 e
e 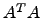 , para várias escolhas de
, para várias escolhas de 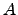 . O que pode conjecturar? Tente provar essas afirmações.
. O que pode conjecturar? Tente provar essas afirmações.
- Considere as matrizes
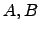 geradas no Octave pelos comandos
geradas no Octave pelos comandos
> A=fix(100*rand(4,4)-50); B=fix(100*rand(4,4)-50);
- Após calcular, para várias escolhas de
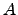 e
e 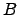 , as matrizes
, as matrizes
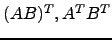 e
e 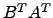 , o que pode inferir?
, o que pode inferir?
- Compare
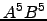 com
com 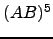 , para várias escolhas de
, para várias escolhas de 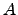 e
e 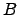 . O que pode concluir?
. O que pode concluir?
- Compare
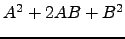 com
com 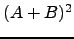 , para várias escolhas de
, para várias escolhas de 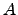 e
e 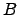 . O que pode concluir?
. O que pode concluir?
- Compare
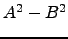 com
com
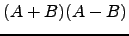 , para várias escolhas de
, para várias escolhas de 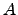 e
e 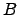 . O que pode concluir?
. O que pode concluir?
- Indique o valor lógico das afirmações seguintes, justificando:
- Se
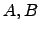 são matrizes quadradas das mesma ordem então
são matrizes quadradas das mesma ordem então
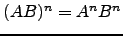
- Se
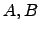 são matrizes quadradas das mesma ordem então
são matrizes quadradas das mesma ordem então
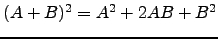
- Se
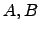 são matrizes quadradas das mesma ordem então
são matrizes quadradas das mesma ordem então
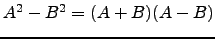
- As matrizes
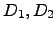 do tipo
do tipo 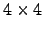 foram geradas aleatoriamente no Octave através das instruções
foram geradas aleatoriamente no Octave através das instruções
> d=fix(100*rand(1,4)-50);
> D1=diag(d);
> d=fix(100*rand(1,4)-50);
> D2=diag(d);
Para várias escolhas de 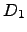 e
e 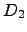 , calcule e procure inferir algo sobre
, calcule e procure inferir algo sobre
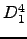 .
.
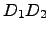 e
e 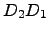
- Para
calcule 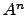 , com
, com 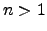 .
.
- Sejam
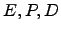 as matrizes
as matrizes 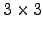 definidas por
definidas por
> I3=eye(3);
> E=I3; E(3,1)=-2;
> P=I3; P(1,:)=I3(2,:); P(2,:)=I3(1,:);
> D=I3; D(2,2)=2;
- Descreva como foram obtidas à custa das linhas/colunas da matriz
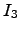
- Indique a inversa de cada uma.
- Considere
![$ A=\left[\begin{array}{ccc}
3 &2 &-1\\
8 & 3 & 3\\
-2 & -1 & -7\end{array}\right]$](img32.png) . Faça os produtos
. Faça os produtos 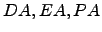 . Relacione-as com
. Relacione-as com 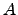 . Recorde o que fez na alínea (a).
. Recorde o que fez na alínea (a).
- Repita a alínea anterior, mas agora com os produtos
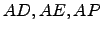 .
.
- Considere as matrizes
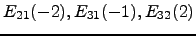 do tipo
do tipo 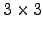 . Considere ainda a matriz
. Considere ainda a matriz
![$ A=\left[\begin{array}{ccc}
5 &1 &-3\\
8 & 0 &-4\\
3 & 0 & 10\end{array}\right]$](img36.png) .
.
- Relacione os produtos
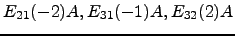 e os produtos
e os produtos
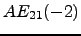 ,
,
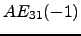 e
e
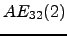 com
com 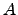 .
.
- Indique uma matriz
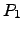 tal que
tal que
![$ P_1A=\left[\begin{array}{ccc}
5 &1 &-3\\
3 & 0 & 10\\
8 & 0 &-4\end{array}\right]$](img42.png) . Verifique no Octave.
. Verifique no Octave.
- Indique uma matriz
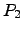 tal que
tal que
![$ AP_2=\left[\begin{array}{ccc}
1 &5 &-3\\
0 & 8 &-4\\
0 & 3 & 10\end{array}\right]$](img44.png) . Verifique no Octave.
. Verifique no Octave.
- Indique uma matriz
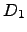 tal que
tal que 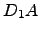 é a matriz obtida de
é a matriz obtida de 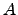 cuja segunda linha surge dividida por 2. Verifique no Octave.
cuja segunda linha surge dividida por 2. Verifique no Octave.
- Indique uma matriz
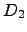 tal que
tal que 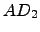 é a matriz obtida de
é a matriz obtida de 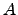 cuja terceira coluna surge multiplicada por 4. Verifique no Octave.
cuja terceira coluna surge multiplicada por 4. Verifique no Octave.
- Considere a matriz
A=[8 2 3; 4 3 2; 1 -2 1].
- Calcule
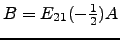 .
.
- Indique uma matriz elementar da forma
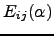 tal que
tal que
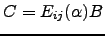 seja uma matriz com as entradas
seja uma matriz com as entradas 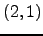 e
e 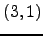 nulas, onde
nulas, onde 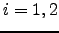 .
.
- Indique uma matriz elementar
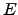 tal que
tal que 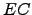 é uma matriz triangular superior.
é uma matriz triangular superior.
- Indique uma matriz invertível
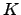 triangular inferior tal que
triangular inferior tal que 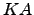 é triangular superior.
é triangular superior.
- Mostre existe uma matriz triangular superior
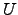 e
e 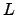 triangular inferior invertível para as quais
triangular inferior invertível para as quais 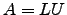 .
.
- Conclua que a matriz
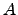 é invertível.
é invertível.
- Considere a matriz
A=[2 4 3; -1 4 0; 3 1 1].
- Indique uma matriz invertível
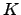 triangular inferior tal que
triangular inferior tal que 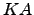 é triangular superior.
é triangular superior.
- Mostre existe uma matriz triangular superior
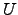 e
e 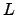 triangular inferior invertível para as quais
triangular inferior invertível para as quais 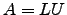 .
.
- Conclua que a matriz
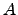 é invertível.
é invertível.
- Considere a matriz
A=[0 2 1; -1 2 1; 1 0 1]
- Indique uma matriz
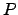 tal que
tal que P*A=[ -1 2 1; 0 2 1; 1 0 1].
- Indique uma matriz invertível
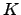 triangular inferior tal que
triangular inferior tal que 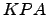 é triangular superior.
é triangular superior.
- Mostre existe uma matriz triangular superior
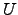 e
e 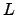 triangular inferior invertível para as quais
triangular inferior invertível para as quais 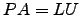 .
.
- Conclua que a matriz
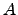 é invertível.
é invertível.
- Mostre que
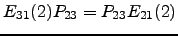 .
.
- Mostre que
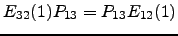 .
.
- Indique uma matriz permutação
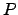 e uma matriz elementar da forma
e uma matriz elementar da forma
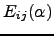 para as quais
para as quais
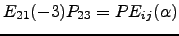 .
.
- Indique uma matriz permutação
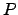 e uma matriz elementar da forma
e uma matriz elementar da forma
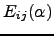 para as quais
para as quais
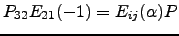 .
.
- Considere a matriz
A=[1 2 3; 2 4 7; -1 1 2].
- Indique uma matriz
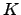 , à custa de produtos de matrizes elementares, tal que
, à custa de produtos de matrizes elementares, tal que 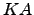 é triangular superior.
é triangular superior.
- Deduza que
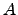 é invertível.
é invertível.
- Factorize
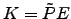 , onde
, onde 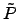 é uma matriz permutação e
é uma matriz permutação e 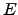 é triangukar inferior.
é triangukar inferior.
- Mostre existe uma matriz permutação
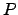 , uma triangular superior
, uma triangular superior 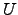 e
e 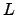 triangular inferior invertível para as quais
triangular inferior invertível para as quais 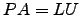 .
.
- Encontre uma factorização da forma
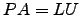 para
para A=[0 1 0 2; 0 -1 0 2; 1 0 0 1].
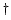 Sejam
Sejam 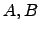 matrizes
matrizes
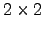 reais tais que
reais tais que
Mostre que 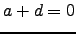 .
.
 Indique todas as matrizes
Indique todas as matrizes 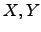 reais
reais
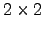 para as quais, simultaneamente,
para as quais, simultaneamente,
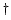 Seja
Seja 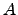 uma matriz
uma matriz
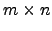 tal que
tal que 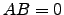 , para todas as matrizes
, para todas as matrizes 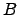 do tipo
do tipo 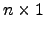 . Mostre que
. Mostre que 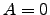 .
.
 Seja
Seja
- Mostre que
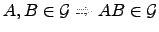 .
.
- Mostre que quaisquer dois elementos de
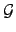 comutam entre si.
comutam entre si.
 Calcule
Calcule
![$ \left[\begin{array}{cc} 17&-6\\ 35&-12\end{array}\right]^ 3$](img82.png) , sabendo que
, sabendo que
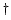 Seja
Seja 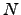 uma matriz
uma matriz
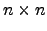 nilpotente, i.e., existe
nilpotente, i.e., existe
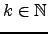 tal que
tal que 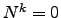 .
.
- Mostre que
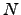 não é invertível.
não é invertível.
- Mostre que
- Se
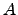 e
e 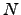 comutam entre si, mostre que
comutam entre si, mostre que 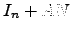 é invertível.
é invertível.
![$\displaystyle A=\left[\begin{array}{cccc}
0&1&0&0\\
0&0&1&0\\
0&0&0&1\\
0&0&0&0 \end{array}\right],$](img26.png)
![$ A=\left[\begin{array}{ccc}
3 &2 &-1\\
8 & 3 & 3\\
-2 & -1 & -7\end{array}\right]$](img32.png) . Faça os produtos
. Faça os produtos ![$ A=\left[\begin{array}{ccc}
5 &1 &-3\\
8 & 0 &-4\\
3 & 0 & 10\end{array}\right]$](img36.png) .
.
![$ P_1A=\left[\begin{array}{ccc}
5 &1 &-3\\
3 & 0 & 10\\
8 & 0 &-4\end{array}\right]$](img42.png) . Verifique no Octave.
. Verifique no Octave.
![$ AP_2=\left[\begin{array}{ccc}
1 &5 &-3\\
0 & 8 &-4\\
0 & 3 & 10\end{array}\right]$](img44.png) . Verifique no Octave.
. Verifique no Octave.
![$\displaystyle AB-BA= \left[\begin{array}{cc}
a & b\\ c&d \end{array}\right].$](img71.png)
![$\displaystyle X+Y= \left[\begin{array}{cc} 1&0\\ 1 &0 \end{array}\right]{\text { e }} X-Y= \left[\begin{array}{cc} 0&1\\ 0 &0 \end{array}\right].$](img74.png)
![$\displaystyle \mathcal{G} = \left\{ \left[\begin{array}{cc} a&b\\ -b&a \end{array}\right]: a,b \in {\mathbb{R}}\right\} .$](img79.png)
![$ \left[\begin{array}{cc} 17&-6\\ 35&-12\end{array}\right]^ 3$](img82.png) , sabendo que
, sabendo que
![$\displaystyle \left[\begin{array}{cc} 17&-6\\ 35&-12\end{array}\right]=\left[\b...
...0 & 3\end{array}\right]\left[\begin{array}{cc} -7& 3\\ 5& -2\end{array}\right].$](img83.png)