Iremos concluir que todas as transformações lineares de
![]() podem ser representadas por matrizes do tipo
podem ser representadas por matrizes do tipo
![]() . Como motivação, consideramos alguns exemplos.
. Como motivação, consideramos alguns exemplos.
Sejam
![]() elementos da base canónica
elementos da base canónica ![]() de
de
![]() e
e
![]() os elementos da base canónica
os elementos da base canónica ![]() de
de
![]() . Seja
ainda
. Seja
ainda
![]() definida por
definida por
Se
![]() , então
, então
![\begin{displaymath}\begin{array}{ccl}
T(x)&=&T(x_1e_1+x_2e_2+x_3e_3)=x_1T(e_1)+x...
...begin{array}{c}x_1\\ x_2\\ x_3\end{array}\right]=Ax
\end{array}\end{displaymath}](img1441.png)
Por outras palavras, a transformação linear definida atrás pode ser representado à custa de uma matriz
![]() , que tem como colunas as coordenadas em relação a
, que tem como colunas as coordenadas em relação a ![]() das imagens dos vectores
das imagens dos vectores
![]() por
por ![]() . Desta forma,
dizemos que nas condições do exemplo anterior, a matriz
. Desta forma,
dizemos que nas condições do exemplo anterior, a matriz ![]() é a
representação matricial de
é a
representação matricial de ![]() relativamente às bases canónicas de
relativamente às bases canónicas de
![]() e
e
![]() .
.
Por exemplo, considere a aplicação linear ![]() definida por
definida por
A matriz que representa ![]() em relação às bases canónicas de
em relação às bases canónicas de
![]() e
e
![]() é
é
![$ A=\left[\begin{array}{ccc}4 & -2 & 3\\ -1 & 5 & -2\end{array}\right]$](img1450.png) . Para todo
. Para todo
![]() ,
, ![]() .
.
Repare que os cálculos envolvidos foram simples de efectuar já que usámos as bases canónicas dos espaços vectoriais. Tal não será, certamente, o caso se usarmos outras bases que não as canónicas. Neste caso, teremos que encontrar as coordenadas das imagens dos elementos da base do primeiro espaço vectorial em relação à base fixada previamente do segundo espaço vectorial. Vejamos o exemplo seguinte:
Sejam
![]() base
base ![]() de
de
![]() e
e
![]() base
base ![]() de
de
![]() . Se
. Se
![]() , então
, então
![]() , e consequentemente
, e consequentemente
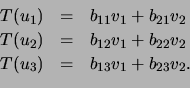
Verificamos, então, que,
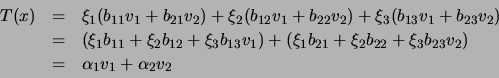
![$\displaystyle \left[\begin{array}{ccc}b_{11}&b_{12}&b_{13}\\ b_{21}&b_{22}&b_{2...
...\end{array}\right]=\left[\begin{array}{c}\alpha_1\\ \alpha_2
\end{array}\right]$](img1464.png)
![$ B=\left[\begin{array}{ccc}b_{11}&b_{12}&b_{13}\\ b_{21}&b_{22}&b_{23}
\end{array}\right]$](img1465.png) é a matriz de
é a matriz de
Passamos de seguida a expôr o caso geral.
Sejam
![]() uma base de
uma base de ![]() ,
,
![]() uma base de
uma base de ![]() , e
, e
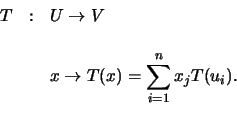
O vector ![]() pode ser escrito - de modo único - como
combinação linear dos vectores
pode ser escrito - de modo único - como
combinação linear dos vectores
![]() .
Assim
.
Assim
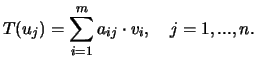
![$ T(x)=\displaystyle\sum_{j=1}^nx_j T(u_j)=
\displaystyle\sum_{j=1}^n[\displayst...
....+\displaystyle\sum_{j=1}^n[a_{mj}x_j]v_m
=\displaystyle\sum_{j=1}^n\varphi v_i$](img1472.png) .
.
Verificamos, assim, que existe entre as coordenadas
![]() de
de ![]() (relativa à base
(relativa à base ![]() ), em
), em ![]() , e as
coordenadas
, e as
coordenadas
![]() de
de ![]() (relativa à base
(relativa à base ![]() ) em
) em ![]() . Tal ligação exprime-se pelas
seguintes equações
. Tal ligação exprime-se pelas
seguintes equações
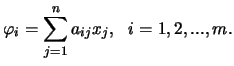
![$\displaystyle \left[\begin{array}{cccc}a_{11}&a_{12}&...&a_{1n}
\\ a_{21}&a_{22...
...[\begin{array}{c}\varphi_1\\ \varphi_2
\\ \vdots\\ \varphi_m
\end{array}\right]$](img1477.png)
Assim, concluímos:
Vimos, então, que dada uma transformação linear
![]() , existe uma matriz
, existe uma matriz
![]() tal que
tal que ![]() . Mais, se
. Mais, se
![]() e
e
![]() são as bases canónicas, respectivamente, de
são as bases canónicas, respectivamente, de
![]() e
e
![]() , então a matriz
, então a matriz ![]() é tal que a coluna
é tal que a coluna ![]() de
de ![]() são as coordenadas de
são as coordenadas de ![]() em relação à base
em relação à base
![]() . No entanto, se se considerarem bases que não as canónicas, então é preciso ter um pouco mais de trabalho.
. No entanto, se se considerarem bases que não as canónicas, então é preciso ter um pouco mais de trabalho.
Por exemplo, considere6.1 a base
![$ A=\left[\begin{array}{cc} 2 & 1\\ 1 & 2\end{array}\right]$](img1496.png) . A matriz que representa
. A matriz que representa
Octave
![\includegraphics[scale=0.3]{Octave_Sombrero.eps}](img64.png)
> v1=[-1;2]; v2=[0;2]; v3=[1; 2]; > A=[2 1; 1 2]; > x1=A\v1 x1 = -1.3333 1.6667 > x2=A\v2 x2 = -0.66667 1.33333 > x3=A\v3 x3 = -1.8952e-16 1.0000e+00 > G=[x1 x2 x3] G = -1.3333e+00 -6.6667e-01 -1.8952e-16 1.6667e+00 1.3333e+00 1.0000e+00
Fixadas as bases dos espaços vectoriais envolvidos, a matriz associada à transformação linear ![]() será, doravante, denotada por
será, doravante, denotada por ![]() .
.
Antes de passarmos ao resultado seguinte, consideremos as transformações lineares
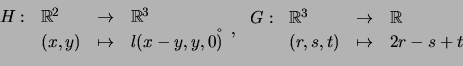
![$\displaystyle \left[\begin{array}{ccc}2&-1&1 \end{array}\right]\left[\begin{array}{c}x-y\\ y\\ 0\end{array}\right]$](img1508.png) |
|||
![$\displaystyle \left[\begin{array}{ccc}2&-1&1 \end{array}\right]\left[\begin{arr...
...& 1 \\ 0 & 0 \end{array}\right]\left[\begin{array}{c} x \\ y \end{array}\right]$](img1509.png) |
|||
![$\displaystyle [G][H] \left[\begin{array}{c}x \\ y \end{array}\right]$](img1510.png) |
Vejamos o que podemos afirmar em geral:
Fechamos, assim, como iniciámos: a algebrização do conjunto das matrizes. As matrizes não são mais do que representantes de um certo tipo de funções (as transformações lineares) entre conjuntos muitos especiais (espaços vectoriais). Se a soma de matrizes corresponde à soma de tranformações lineares (em que a soma de funções está definida como a função definida pela soma das imagens), o produto de matrizes foi apresentado como uma operação bem mais complicada de efectuar. No entanto, a forma como o produto matricial foi definido corresponde à composição das transformações lineares definidas pelas matrizes.
Este último capítulo explica, ainda, a razão pela qual não demos ênfase a espaços vectoriais reais de dimensão finita que não os da forma
![]() . Mostrámos que todo o espaço vectorial finitamente gerado (ou seja, que tenha uma base com um número finito de elementos) é isomorfo a algum
. Mostrámos que todo o espaço vectorial finitamente gerado (ou seja, que tenha uma base com um número finito de elementos) é isomorfo a algum
![]() . Já os não finitamente gerados pertencem a outra divisão: são bem mais difíceis de estudar, mas em compensação têm aplicações fantásticas, como o processamento digital de imagem.
. Já os não finitamente gerados pertencem a outra divisão: são bem mais difíceis de estudar, mas em compensação têm aplicações fantásticas, como o processamento digital de imagem.
Como epílogo, deixamos a seguinte mensagem: a parte interessante da matemática só agora está a começar!
![]()
![]()
![]()
![]()
Seguinte: Bibliografia
Acima: Transformações lineares
Anterior: Propriedades das transformações lineares
Conteúdo
Pedro Patricio
2008-01-08