Regra de Cramer

A regra de Cramer fornece-nos um processo de cálculo da solução de uma equação consistente $Ax=b$ quando $A$ é invertível, e portanto a solução é única.

Dada a equação $Ax=b$, onde $A$ é $n\times n$ não-singular, $x=\left[\begin{array}{c}x_1 x_2 \vdots x_n\end{array}\right]$ e $b$ é do tipo $n\times 1$, denote-se por $A^{(i)}$ a matriz obtida de $A$ substituindo a coluna $i$ de $A$ pela coluna $b$.

Teorema 3.4.1 (Regra de Cramer)   Nas condições do parágrafo anterior, a única solução de $Ax=b$ é dada por

$$x_i=\frac{\vert A^{(i)}\vert}{\vert A\vert}.$$

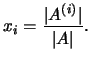
Octave
Vamos aplicar a regra de Cramer:

> A=[1 -2 1; 1 1 0; -2 1 -2];
> b=[1;1;-1];

A matriz $A$ é invertível, e portanto $Ax=b$ é uma equação consistente com uma única solução:

> det(A)
ans = -3

Definamos as matrizes A1,A2,A3 como as matrizes $A^{(1)}, A^{(2)}, A^{(3)}$, respectivamente. Aplicamos, de seguida, a regra de Cramer.

> A1=A; A1(:,1)=b; A2=A; A2(:,2)=b; A3=A; A3(:,3)=b;
> x1=det(A1)/det(A)
x1 = 1.3333
> x2=det(A2)/det(A)
x2 = -0.33333
> x3=det(A3)/det(A)
x3 = -1

Os valores obtidos formam, de facto, a solução pretendida:

> A*[x1;x2;x3]
ans =

   1
   1
  -1