- Se
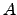 tem uma linha ou uma coluna nula então
tem uma linha ou uma coluna nula então 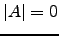 .
.
 .
.
- Se
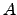 é triangular (inferior ou superior) então
é triangular (inferior ou superior) então
 .
.
-
 com
com  .
.
São consequência da definição os resultados que de seguida apresentamos, dos quais omitimos a demonstração.
 .
.
Daqui segue que ![]() . Segue também que dada uma matriz tringular (inferior ou superior) que esta é invertível se e só se tiver determinante não nulo. Mais adiante, apresentaremos um resultado que generaliza esta equivalência para matrizes quadradas não necessariamente triangulares.
. Segue também que dada uma matriz tringular (inferior ou superior) que esta é invertível se e só se tiver determinante não nulo. Mais adiante, apresentaremos um resultado que generaliza esta equivalência para matrizes quadradas não necessariamente triangulares.
Como
![]() e
e
![]() , segue que
, segue que
![]() ,
,
![]() e que
e que
![]() . Repare ainda que, se
. Repare ainda que, se ![]() é
é ![]() , é válida a igualdade
, é válida a igualdade
![]() , já que
, já que
![]() . De forma análoga, dada uma matriz diagonal
. De forma análoga, dada uma matriz diagonal ![]() com elementos diagonais
com elementos diagonais
![]() , tem-se
, tem-se
![]() .
.
O corolário anterior é passível de ser generalizado considerando não linhas iguais, mas tal que uma linha se escreva como soma de múltiplos de outras linhas. O mesmo se aplica a colunas.
Sabendo que uma matriz é invertível se e só se a matriz escada associada (por aplicação de Gauss) é invertível, e que esta sendo triangular superior é invertível se e só se os seus elementos diagonais são todos nulos, segue que, e fazendo uso de resultados enunciados e provados anteriormente,
Portanto, uma matriz com duas linhas/colunas iguais não é invertível. Mais, uma matriz que tenha uma linha que se escreva como soma de múltiplos de outras das suas linhas não é invertível.
Suponha que ![]() é invertível.
é invertível.
Existem matrizes elementares
![]() e uma matriz escada (de linhas)
e uma matriz escada (de linhas) ![]() tal que
tal que
![]() . Ora existem também
. Ora existem também
![]() matrizes elementares, e
matrizes elementares, e ![]() matriz escada de linhas para as quais
matriz escada de linhas para as quais
![]() . Note que neste último caso se pode assumir que não houve trocas de linhas, já que os pivots do AEG são os elementos diagonais de
. Note que neste último caso se pode assumir que não houve trocas de linhas, já que os pivots do AEG são os elementos diagonais de ![]() já que
já que ![]() é triangular inferior, que são não nulos por
é triangular inferior, que são não nulos por ![]() ser invertível. Ora
ser invertível. Ora ![]() é então uma matriz triangular superior que se pode escrever como produto de matrizes triangulares inferiores, e portanto
é então uma matriz triangular superior que se pode escrever como produto de matrizes triangulares inferiores, e portanto ![]() é uma matriz diagonal. Seja
é uma matriz diagonal. Seja ![]() . Resumindo,
. Resumindo,
![]() . Recorde que, dada uma matriz elementar
. Recorde que, dada uma matriz elementar ![]() , é válida
, é válida
![]() . Então,
. Então,
Como ![]() , segue do teorema anterior a relação entre o determinante uma matriz invertível com o da sua inversa.
, segue do teorema anterior a relação entre o determinante uma matriz invertível com o da sua inversa.

Recorde que para que uma matriz ![]() seja invertível exige-se a existência de uma outra
seja invertível exige-se a existência de uma outra ![]() para a qual
para a qual ![]() . O resultado seguinte mostra que se pode prescindir da verificação de uma das igualdades.
. O resultado seguinte mostra que se pode prescindir da verificação de uma das igualdades.
Para mostrar que ![]() , repare que como
, repare que como ![]() então
então ![]() é invertível, e portanto
é invertível, e portanto
![]() , donde
, donde ![]() .
.
Faça a identificação dos vectores
![]() com as matrizes coluna
com as matrizes coluna
![$ \left[\begin{array}{c}a b\end{array}\right]$](img555.png) . O produto interno usual
. O produto interno usual
![]() em
em
![]() pode ser encarado como o produto matricial
pode ser encarado como o produto matricial
![$ \left[\begin{array}{cc} u_1 &u_2\end{array}\right]\left[\begin{array}{c}v_1 v_2\end{array}\right]$](img558.png) . Ou seja,
. Ou seja,
![]() . Esta identificação e noção pode ser generalizada de forma trivial para
. Esta identificação e noção pode ser generalizada de forma trivial para
![]() . Dois vectores
. Dois vectores ![]() e
e ![]() de
de
![]() dizem-se ortogonais,
dizem-se ortogonais, ![]() , se
, se
![]() . A norma usual em
. A norma usual em
![]() é definida por
é definida por
![]() , com
, com
![]()
![$ A=\left[\begin{array}{ccc}
c_1 & \cdots & c_n \end{array}\right]$](img570.png) , temos que
, temos que
![$\displaystyle I_n= A^TA= \left[\begin{array}{c} c_1^T c_2^T \vdots c_n...
...}\right]
\left[\begin{array}{cccc}
c_1 & c_2 & \cdots & c_n \end{array}\right].$](img571.png)
![$ \left[\begin{array}{c} c_1^T c_2^T \vdots c_n^T \end{array}\right]
\left[\begin{array}{cccc}
c_1 & c_2 & \cdots & c_n \end{array}\right]$](img572.png) é
é Ou seja, as colunas das matrizes ortogonais são ortogonais duas a duas. O mesmo se pode dizer acerca das linhas, já que a transposta de uma matriz ortogonal é de novo uma matriz ortogonal.
![]()
![]()
![]()
![]()
Seguinte: Teorema de Laplace
Acima: Determinantes
Anterior: Definição
Conteúdo
Pedro Patricio
2008-01-08