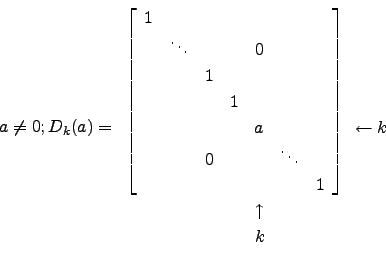
Nesta secção, iremos apresentar um tipo de matrizes que terão um papel relevante em resultados vindouros: as matrizes elementares. Estas dividem-se em três tipos:
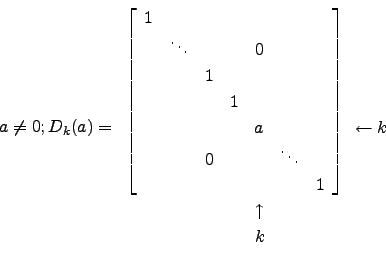
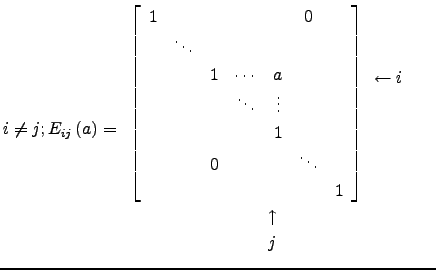
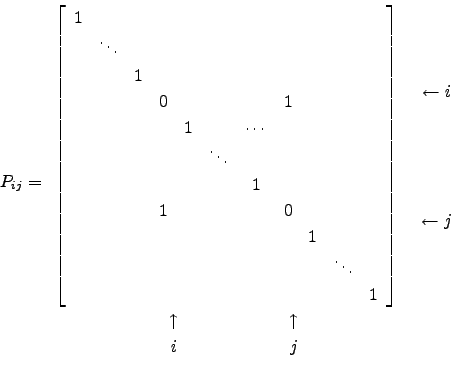
Ou seja, as matrizes elementares de ordem ![]() são obtidas da matriz identidade
são obtidas da matriz identidade ![]() fazendo:
fazendo:
É óbvio que
![]() .
.
A primeira propriedade que interessa referir sobre estas matrizes é que são invertíveis. Mais, para
![]() ,
,
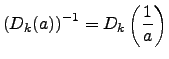
A segunda, relevante para o que se segue, indica outro o modo de se obter as matrizes ![]() e
e ![]() da matriz identidade, cujas linhas são denotadas por
da matriz identidade, cujas linhas são denotadas por
![]() :
:
Aplicando o mesmo raciocínio, mas considerando as colunas
![]() da matriz identidade:
da matriz identidade:
Octave
![\includegraphics[scale=0.3]{Octave_Sombrero.eps}](img64.png)
Considere as matrizes ![]() elementares
elementares
![]() . Recorde que a matriz
. Recorde que a matriz ![]() é dada por eye(3).
é dada por eye(3).
> D=eye(3); > D(2,2)=5; > D D = 1 0 0 0 5 0 0 0 1 > E=eye(3); > E(2,3)=3; > E E = 1 0 0 0 1 3 0 0 1 > I3=eye(3); > P=I3; > P(1,:)=I3(3,:); P(3,:)=I3(1,:); > P P = 0 0 1 0 1 0 1 0 0Nesta última matriz, as instruções P(1,:)=I3(3,:); P(3,:)=I3(1,:); indicam que a primeira linha de
O que sucede se, dada uma matriz ![]() , a multiplicarmos à esquerda ou à direita2.2 por uma matriz elementar? Vejamos com alguns exemplos, tomando
, a multiplicarmos à esquerda ou à direita2.2 por uma matriz elementar? Vejamos com alguns exemplos, tomando
![$\displaystyle A=\left[\begin{array}{ccc}
4 &2 &0\\
1 & 1 & 0\\
2 & -1 & 4\end{array}\right], P=P_{12}, E=E_{31}(-2), D=D_2\left(\frac{1}{2}\right).$](img299.png)
Octave
![\includegraphics[scale=0.3]{Octave_Sombrero.eps}](img64.png)
Vamos então definir as matrizes A,P,E,D no Octave:
> A=[4 2 0; 1 1 0; 2 -1 4]; > I3=eye(3); > E=I3; E(3,1)=-2; > P=I3; P(1,:)=I3(2,:); P(2,:)=I3(1,:); > D=I3; D(2,2)=1/2;Façamos o produto
> P*A ans = 1 1 0 4 2 0 2 -1 4
Qual a relação entre ![]() e
e ![]() ? Repare que ocorreu uma troca da primeira e da segunda linha de
? Repare que ocorreu uma troca da primeira e da segunda linha de ![]() . Que por sinal foram as mesmas trocas que se efectuaram a
. Que por sinal foram as mesmas trocas que se efectuaram a ![]() de forma a obtermos
de forma a obtermos ![]() .
.
À matriz ![]() , multiplicamo-la, à esquerda, por
, multiplicamo-la, à esquerda, por ![]() :
:
> E*P*A ans = 1 1 0 4 2 0 0 -3 4
> D*E*P*A
ans =
1 1 0
2 1 0
0 -3 4
Uma matriz permutação de ordem ![]() é uma matriz obtida de
é uma matriz obtida de ![]() à custa de trocas de suas linhas (ou colunas). Aqui entra o conceito de permutação. Uma permutação no conjunto
à custa de trocas de suas linhas (ou colunas). Aqui entra o conceito de permutação. Uma permutação no conjunto
![]() é uma bijecção (ou seja, uma aplicação simultaneamente injectiva e sobrejectiva) de
é uma bijecção (ou seja, uma aplicação simultaneamente injectiva e sobrejectiva) de ![]() em
em ![]() . Uma permutação
. Uma permutação
![]() pode ser representada pela tabela
pode ser representada pela tabela
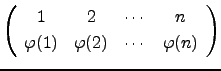 . Para simplificar a escrita, é habitual omitir-se a primeira linha, já que a posição da imagem na segunda linha indica o (único) objecto que lhe deu origem.
. Para simplificar a escrita, é habitual omitir-se a primeira linha, já que a posição da imagem na segunda linha indica o (único) objecto que lhe deu origem.
Como exemplo, considere a permutação
![]() . Tal significa que
. Tal significa que
Note que ![]() tem
tem
![]() elementos. De facto, para
elementos. De facto, para
![]() ,
, ![]() pode tomar
pode tomar ![]() valores distintos. Mas
valores distintos. Mas ![]() apenas pode tomar um dos
apenas pode tomar um dos ![]() restantes, já que não se podem repetir elementos. E assim por diante. Obtemos então
restantes, já que não se podem repetir elementos. E assim por diante. Obtemos então ![]() permutações distintas.
permutações distintas.
Dada a permutação
![]() , se
, se
![]() e
e ![]() então
então ![]() diz-se uma inversão de
diz-se uma inversão de ![]() . Na permutação
. Na permutação
![]() acima exemplificada existem três inversões, já que
acima exemplificada existem três inversões, já que
![]() . O sinal de uma permutação
. O sinal de uma permutação ![]() , denotado por
, denotado por
![]() , toma o valor
, toma o valor ![]() caso o número de inversões seja par, e
caso o número de inversões seja par, e ![]() caso contrário. Portanto,
caso contrário. Portanto,
![]() . As permutações com sinal
. As permutações com sinal ![]() chamam-se permutações pares (e o conjunto por elas formado chama-se grupo alterno,
chamam-se permutações pares (e o conjunto por elas formado chama-se grupo alterno, ![]() ), e as cujo sinal é
), e as cujo sinal é ![]() denominam-se por permutações ímpares.
denominam-se por permutações ímpares.
Uma transposição é uma permutação que fixa todos os pontos à excepção de dois. Ou seja,
![]() é uma transposição se existirem
é uma transposição se existirem ![]() distintos para os quais
distintos para os quais
![]() e
e ![]() para todo o
para todo o ![]() diferente de
diferente de ![]() e
e ![]() . Verifica-se que toda a permutação
. Verifica-se que toda a permutação ![]() se pode escrever como composição de transposições
se pode escrever como composição de transposições
![]() . Ou seja,
. Ou seja,
![]() . Esta decomposição não é única, mas quaisquer duas decomposições têm a mesma paridade de transposições. Ou seja, se existe uma decomposição com um número par [resp. ímpar] de intervenientes, então qualquer outra decomposição tem um número par [resp. ímpar] de transposições. Mais, esse número tem a mesma paridade da do número de inversões. Por consequência, o sinal de qualquer transposição é
. Esta decomposição não é única, mas quaisquer duas decomposições têm a mesma paridade de transposições. Ou seja, se existe uma decomposição com um número par [resp. ímpar] de intervenientes, então qualquer outra decomposição tem um número par [resp. ímpar] de transposições. Mais, esse número tem a mesma paridade da do número de inversões. Por consequência, o sinal de qualquer transposição é ![]() .
A permutação
.
A permutação ![]() definida atrás pode-se decompor como
definida atrás pode-se decompor como
![]() .
.
O conjunto das permutações ![]() pode ser identificado com o conjunto das matrizes permutação de ordem
pode ser identificado com o conjunto das matrizes permutação de ordem ![]() , em que a composição de permutação é de uma forma natural identificado com o produto de matrizes. A matriz permutação
, em que a composição de permutação é de uma forma natural identificado com o produto de matrizes. A matriz permutação ![]() associada à permutação
associada à permutação ![]() é a matriz obtida de
é a matriz obtida de ![]() realizando as trocas de linhas segundo
realizando as trocas de linhas segundo ![]() . Para fácil compreensão, vamos recorrer ao Octave.
. Para fácil compreensão, vamos recorrer ao Octave.
Octave
![\includegraphics[scale=0.3]{Octave_Sombrero.eps}](img64.png)
> I5=eye(5); > P=I5([2 1 5 3 4], :) P = 0 1 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0
Na primeira linha de ![]() surge a segunda de
surge a segunda de ![]() , na segunda a primeira, na terceira a quinta de
, na segunda a primeira, na terceira a quinta de ![]() , e assim por diante.
, e assim por diante.
De facto, toda a matriz permutação pode-se escrever como produto de matrizes da forma ![]() , tal como definidas atrás. Tal é consequência da existência de uma decomposição da permutação em transposições. Note que as transposições se identificam com as matrizes
, tal como definidas atrás. Tal é consequência da existência de uma decomposição da permutação em transposições. Note que as transposições se identificam com as matrizes ![]() . Voltemos ao Octave e ao exemplo acima:
. Voltemos ao Octave e ao exemplo acima:
Octave
![\includegraphics[scale=0.3]{Octave_Sombrero.eps}](img64.png)
Em primeiro lugar, definamos as matrizes associadas às transposições, e façamos o seu produto:
> P1=I5([2 1 3 4 5], :); > P2=I5([1 2 5 4 3], :); > P3=I5([1 2 4 3 5], :); > P1*P2*P3 ans = 0 1 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0O produto iguala a matriz
> all(all(P==P1*P2*P3)) ans = 1
Operações elementares sobre as linhas de ![]() são as que resultam pela sua multiplicação à esquerda por matrizes elementares. Ou seja, são operações elementares por linhas de uma matriz
são as que resultam pela sua multiplicação à esquerda por matrizes elementares. Ou seja, são operações elementares por linhas de uma matriz
De forma análoga se definem as operações elementares sobre as colunas de uma matriz, sendo a multiplicação por matrizes elementares feita à direita da matriz. Na prática, tal resulta em substituir a palavra ``linha'' pela palavra ``coluna'' na descrição acima.
Considere a matriz
![$ A=\left[\begin{array}{ccc} 2& 4 &6 1& 4& 2 -1 &0& 1\end{array}\right]$](img338.png) .
Em primeiro lugar, e efectuando operações elementares nas linhas de
.
Em primeiro lugar, e efectuando operações elementares nas linhas de ![]() , tentaremos obter zeros por debaixo da entrada
, tentaremos obter zeros por debaixo da entrada ![]() . Ou seja, pretendemos obter algo como
. Ou seja, pretendemos obter algo como
![$ \left[\begin{array}{ccc}
2 & 4 & 6\\
0 & ? & ?\\
0 & ? & ?\end{array}\right]$](img340.png) . Substitua-se a segunda linha,
. Substitua-se a segunda linha, ![]() , pela sua soma com o simétrico de metade da primeira. Ou seja,
, pela sua soma com o simétrico de metade da primeira. Ou seja,
![$\displaystyle \left[\begin{array}{ccc} 2& 4 &6 1& 4& 2 -1 &0& 1\end{array}\...
...2}l_1} \left[\begin{array}{ccc} 2& 4 &6 0& 2& -1 -1 &0& 1\end{array}\right]$](img342.png)
![$ E_{21}(-\frac{1}{2})=\left[\begin{array}{ccc}1 & 0&0\\
-\frac{1}{2}&1&0\\
0&0&1\end{array}\right]$](img343.png) . Façamos o mesmo raciocínio para a terceira linha:
. Façamos o mesmo raciocínio para a terceira linha:
![$\displaystyle \left[\begin{array}{ccc} 2& 4 &6 1& 4& 2 -1 &0& 1\end{array}\...
...}{2}l_1} \left[\begin{array}{ccc} 2 & 4 &6\\
0&2&-1\\
0&2&4\end{array}\right]$](img344.png)
![$\displaystyle E_{31}(\frac{1}{2})E_{21}(-\frac{1}{2})A=\left[\begin{array}{ccc} 2 & 4 &6\\
0&2&-1\\
0&2&4\end{array}\right]=B.$](img346.png)
Todos os elementos na primeira coluna de ![]() , à excepção de
, à excepção de ![]() , são nulos. Concentremo-nos agora na segunda coluna, e na segunda linha. Pretendem-se efectuar operações elementares nas linhas de
, são nulos. Concentremo-nos agora na segunda coluna, e na segunda linha. Pretendem-se efectuar operações elementares nas linhas de ![]() por forma a obter uma matriz da forma
por forma a obter uma matriz da forma
![$ \left[\begin{array}{ccc}
2 & 4 & 6\\
0 & 2 & -1\\
0 & 0 & ?\end{array}\right]$](img348.png) . Para tal,
. Para tal,
![$\displaystyle \left[\begin{array}{ccc} 2 & 4 &6\\
0&2&-1\\
0&2&4\end{array}\r...
...l_2}
\left[\begin{array}{ccc} 2 & 4 &6\\
0&2&-1\\
0&0&3\end{array}\right]=U.$](img349.png)
![$\displaystyle E_{32}(-1)E_{31}(\frac{1}{2})E_{21}(-\frac{1}{2})A=U=\left[\begin{array}{ccc} 2 & 4 &6\\
0&2&-1\\
0&0&3\end{array}\right]$](img353.png)
Octave
![\includegraphics[scale=0.3]{Octave_Sombrero.eps}](img64.png)
Consideremos a matriz A dada por
> A=[2 4 6;2 2 2;-1 0 1];À segunda linha de
> I3=eye(3); E21=I3; E21(2,1)=-1; > A2=E21*A A2 = 2 4 6 0 -2 -4 -1 0 1À terceira, somamos a primeira multiplicada por
> E31=I3; E31(3,1)=0.5; > A3=E31*A2 ans = 2 4 6 0 -2 -4 0 2 4Finalmente, à terceira somamos a segunda linha:
> E32=I3; E32(3,2)=1; > A4=E32*A3 A4 = 2 4 6 0 -2 -4 0 0 0A matriz A4 obtida é triangular superior, com um elemento diagonal nulo. Logo, a matriz inicial
O Octave contém o algoritmo numa sua rotina:
> [l,u,p]=lu(A) l = 1.00000 0.00000 0.00000 1.00000 1.00000 0.00000 -0.50000 -1.00000 1.00000 u = 2 4 6 0 -2 -4 0 0 0 p = 1 0 0 0 1 0 0 0 1Aqui, u indica a matriz final do algoritmo e l a inversa do produto das matrizes elementares da forma
> (E32*E31*E21)^-1A matriz p é neste caso a identidade, e não tem nenhum papel. Mais à frente veremos a importância desta matriz (quando não é a identidade).
Obtivemos, então, a factorização lu=A.
O exemplo escolhido foi, de facto, simples na aplicação. Alguns passos podem não ser possíveis, nomeadamente o primeiro. Repare que o primeiro passo envolve uma divisão (no nosso caso, dividimos a linha 1 por ![]() ). A propósito, os elementos-chave na divisão, ou de forma mais clara, o primeiro elemento não nulo da linha a que vamos tomar um seu múltiplo denomina-se por pivot. Ora esse pivot tem que ser não nulo. E se for nulo? Nesse caso, trocamos essa linha por outra mais abaixo que tenha, nessa coluna, um elemento não nulo. E se todos forem nulos? Então o processo terminou para essa coluna e consideramos a coluna seguinte. Apresentamos dois exemplos, um para cada um dos casos descritos:
). A propósito, os elementos-chave na divisão, ou de forma mais clara, o primeiro elemento não nulo da linha a que vamos tomar um seu múltiplo denomina-se por pivot. Ora esse pivot tem que ser não nulo. E se for nulo? Nesse caso, trocamos essa linha por outra mais abaixo que tenha, nessa coluna, um elemento não nulo. E se todos forem nulos? Então o processo terminou para essa coluna e consideramos a coluna seguinte. Apresentamos dois exemplos, um para cada um dos casos descritos:
![$\displaystyle \left[\begin{array}{ccc}0 & 1 &2\\
1& 1 & 2\\
-3& 2 &9\end{arra...
...\left[\begin{array}{ccc}0 & 1 & 1\\
0 & 6 & 7\\
0 & 1 & -2\end{array}\right].$](img359.png)
Apresentamos, de seguida, o algoritmo de eliminação de Gauss de uma forma mais formal.
![]()
![]()
![]()
![]()
Seguinte: O Algoritmo de Eliminação
Acima: Um resultado de factorização
Anterior: Um resultado de factorização
Conteúdo
Pedro Patricio
2008-01-08