


Seguinte: Sobre este documento ...
Universidade do Minho
L.E.M., L.M.C.C. - 4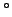 ano
ano
Departamento de Matemática
Mat. (Esp. Ensino), L.C.C. - 3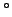 ano
ano
Teoria de Números Computacional
folha vi
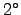 semestre, 2006/2007
semestre, 2006/2007
- Encontre um sistema reduzido de resíduos dos inteiros
(a) 6 (b) 9 (c) 10 (d) 14 (e) 16 (f)17
- Use o Teorema de Euler para encontrar o resto da divisão de
 por 35.
por 35.
- Use o Teorema de Euler para encontrar o último algarismo de
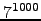 na representação na base decimal.
na representação na base decimal.
- Use o Teorema de Euler para encontrar o último símbolo na expansão hexadecimal de
 .
.
- Fazendo uso do Teorema de Euler, resolva as congruências lineares
(a)
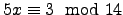 (b)
(b)
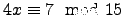 (c)
(c)
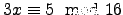
- Calcule
 para
para
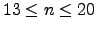 .
.
- Calcule
 com
com 
(a) 100 (b) 256 (c) 1001
(d)
 (e)
(e) 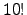 (f)
(f) 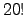
- Mostre que existe uma infinidade de primos, usando a função
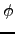 de Euler.
de Euler.
[Sugestão: suponha que o conjunto
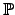 dos números primos é finito, e considere
dos números primos é finito, e considere
 . Conclua que
. Conclua que 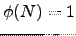 .]
.]
- Lehmer conjecturou que
 é primo se
é primo se  divide
divide  . Teste a conjectura, usando o pari/gp.
. Teste a conjectura, usando o pari/gp.
[Sugestão: for(i=2,N,n=2*i+1;if((n-1)%eulerphi(n)==0&&!isprime(n),print(n))), para  suficientemente grande.]
suficientemente grande.]
- Encontre os primos
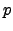 e
e 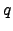 , sabendo que
, sabendo que
 e
e
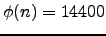 .
.
- Encontre os primos
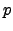 e
e 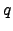 , sabendo que
, sabendo que
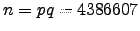 e
e
 .
.
- Suponha que um criptanalista encontra um certo
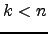 que não é primo relativo com
que não é primo relativo com 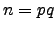 usado no RSA. Mostre que o criptanalista pode quebrar a cifra. Calcule a probabilidade de tal acontecer.
usado no RSA. Mostre que o criptanalista pode quebrar a cifra. Calcule a probabilidade de tal acontecer.



Seguinte: Sobre este documento ...
Pedro Patricio
2007-05-22
![]() ano
ano
![]() semestre, 2006/2007
semestre, 2006/2007