Some applications of Buchholz's Omega rule
(Abstract)
Thierry Coquand
The goal of the course will be to present some concepts and
methods of proof theory, centred around various applications of
the so-called 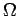 -rule.
The negative translation due to Kolmogorov 1925, and rediscovered
by Godel and Gentzen 1932, shows that one can reduce the classical
theory of first-order arithmetic to its intuitionistic version.
One can argue that this is a positive solution to Hilbert's
program (and it is actually interesting to understand the
connection with Godel second incompletness theorem). Similar
translations work for other systems, for instance, second-order
arithmetic. However, there are cases where such a translation
cannot be applied. In some cases, this is because the classical
version is strictly more powerful from a proof-theoretic point of
view, and hence one cannot have a syntactical translation in the
intuitionistic version. But in other cases, the negative
translation does not work and it can be shown that the
classical and intuitionistic versions have the same
proof-theoretical power. One example is arithmetic restricted to
-rule.
The negative translation due to Kolmogorov 1925, and rediscovered
by Godel and Gentzen 1932, shows that one can reduce the classical
theory of first-order arithmetic to its intuitionistic version.
One can argue that this is a positive solution to Hilbert's
program (and it is actually interesting to understand the
connection with Godel second incompletness theorem). Similar
translations work for other systems, for instance, second-order
arithmetic. However, there are cases where such a translation
cannot be applied. In some cases, this is because the classical
version is strictly more powerful from a proof-theoretic point of
view, and hence one cannot have a syntactical translation in the
intuitionistic version. But in other cases, the negative
translation does not work and it can be shown that the
classical and intuitionistic versions have the same
proof-theoretical power. One example is arithmetic restricted to
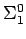 induction. Another example is the so-called theory of
finitely iterated inductive definitions. Buchholz found a general
technique, called the
induction. Another example is the so-called theory of
finitely iterated inductive definitions. Buchholz found a general
technique, called the 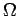 -rule, to show in this case that the
strength of the classical version is the same as the
intuitionistic version. This method can be presented as a
refinement of the negative translation, and can be applied to
other frameworks, for instance
-rule, to show in this case that the
strength of the classical version is the same as the
intuitionistic version. This method can be presented as a
refinement of the negative translation, and can be applied to
other frameworks, for instance 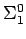 induction. A similar
method applies also to reduce some fragment of second-order
arithmetic to intuitionistic theory of inductive definitions. This
can be presented in a suggestive way as an analysis of some
fragment of system F and we describe in particular a natural
fragment of system F which has the same strength as first-order
arithmetic.
induction. A similar
method applies also to reduce some fragment of second-order
arithmetic to intuitionistic theory of inductive definitions. This
can be presented in a suggestive way as an analysis of some
fragment of system F and we describe in particular a natural
fragment of system F which has the same strength as first-order
arithmetic.