The Curry/Howard correspondence and some of its extensions to sequent calculus
(Abstract)
José Espírito Santo - Luís Pinto
The Curry/Howard correspondence, in
its simplest form, establishes a connection between natural
deduction for implicational intuitionistic logic and the simply
typed 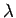 -calculus. In this course, we present some
experiments in the attempt to obtain an analogous correspondence
between sequent calculi and appropriate extensions of the simply
typed
-calculus. In this course, we present some
experiments in the attempt to obtain an analogous correspondence
between sequent calculi and appropriate extensions of the simply
typed 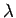 -calculus.
We review natural deduction and sequent calculus for
intuitionistic logic, with emphasis on two issues: (i)
permutability of inferences in sequent calculus and the
permutability theorem establishing that two sequent calculus
derivations may be interpreted as the same natural deduction proof
iff they are inter-permutable; (ii) the relationship between
normalisation and cut-elimination. We make precise the
Curry/Howard correspondence, showing how to read the typing system
and
-calculus.
We review natural deduction and sequent calculus for
intuitionistic logic, with emphasis on two issues: (i)
permutability of inferences in sequent calculus and the
permutability theorem establishing that two sequent calculus
derivations may be interpreted as the same natural deduction proof
iff they are inter-permutable; (ii) the relationship between
normalisation and cut-elimination. We make precise the
Curry/Howard correspondence, showing how to read the typing system
and 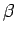 -reduction of the simply typed
-reduction of the simply typed 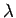 -calculus as a
natural deduction system (with term annotations to represent
proofs) and its normalisation procedure. We survey some of the
attempts to extend the Curry/Howard correspondence to sequent
calculus, with special focus on Herbelin's work. We argue that
these approaches do not address directly the permutability
phenomenon in sequent calculus.
We present a system, the generalised multiary
-calculus as a
natural deduction system (with term annotations to represent
proofs) and its normalisation procedure. We survey some of the
attempts to extend the Curry/Howard correspondence to sequent
calculus, with special focus on Herbelin's work. We argue that
these approaches do not address directly the permutability
phenomenon in sequent calculus.
We present a system, the generalised multiary 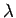 -calculus,
which is an extension of the simply typed
-calculus,
which is an extension of the simply typed 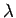 -calculus where
application is generalised in two directions: (i) ``generality'',
in the sense of von Plato's generalised eliminations; and (ii)
``multiarity'', i.e. the ability to apply functions to lists of
arguments. We show how to view this system as a sequent calculus
with term annotations, where the rule for typing the new form of
application, when viewed as an inference rule, encompasses both a
form of left introduction and a class of cuts. Our approach has an
account of the permutability phenomenon in that the generalised
multiary
-calculus where
application is generalised in two directions: (i) ``generality'',
in the sense of von Plato's generalised eliminations; and (ii)
``multiarity'', i.e. the ability to apply functions to lists of
arguments. We show how to view this system as a sequent calculus
with term annotations, where the rule for typing the new form of
application, when viewed as an inference rule, encompasses both a
form of left introduction and a class of cuts. Our approach has an
account of the permutability phenomenon in that the generalised
multiary 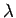 -calculus comes equipped with a confluent and
strongly normalising set of permutations, for which the
permutability theorem holds.
-calculus comes equipped with a confluent and
strongly normalising set of permutations, for which the
permutability theorem holds.