Implicit characterizations of complexity classes
(Abstract)
Isabel Oitavem
Several machine independent approaches to relevant classes of
computational complexity have been developed. All them lead to
characterizations of classes of computational complexity where the
machine formulation and resources are implicit -- implicit
characterizations. Conceptually, implicit characterizations link
computational complexity to levels of definitional and inferential
abstractions of significant independent interest.
In this course we focus on the class of functions computable in
polynomial time,
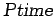 . The first machine independent
characterization of
. The first machine independent
characterization of
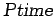 was given by Cobham in 1964. There are
several nuances of the Cobham characterization, but all them use
bounded recursion schemes which address to the resource constraints of
was given by Cobham in 1964. There are
several nuances of the Cobham characterization, but all them use
bounded recursion schemes which address to the resource constraints of
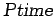 . Several years later, in 1992, Bellantoni and Cook came up
with a remarkable characterization of
. Several years later, in 1992, Bellantoni and Cook came up
with a remarkable characterization of
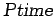 , where the use
of input-sorted functions avoid the use of explicit bounds. In the
same vein, but using two-sorted functions, Leivant
also achieved a bound-free characterization of
, where the use
of input-sorted functions avoid the use of explicit bounds. In the
same vein, but using two-sorted functions, Leivant
also achieved a bound-free characterization of
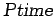 .
We describe and discuss these characterizations of
.
We describe and discuss these characterizations of
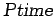 . In
particular, we show that by removing the bounds on the Cobham's recursion
scheme one gets functions of exponential growth. The aim of this
course is to illustrate how sorted approaches can be used to build, in
the classes, resource-independent mechanisms to control the growth of
the functions. If the time allows we will extend this course to other
classes of complexity.
. In
particular, we show that by removing the bounds on the Cobham's recursion
scheme one gets functions of exponential growth. The aim of this
course is to illustrate how sorted approaches can be used to build, in
the classes, resource-independent mechanisms to control the growth of
the functions. If the time allows we will extend this course to other
classes of complexity.