


Seguinte: Sobre este documento ...
Universidade do Minho
L.E.M., L.M.C.C. - 4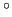 ano
ano
Departamento de Matemática
Mat. (Esp. Ensino), L.C.C. - 3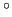 ano
ano
Teoria de Números Computacional
folha ii
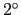 semestre, 2006/2007
semestre, 2006/2007
- Recorde a sucessão de Fibonacci
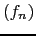 :
:
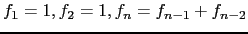 , para
, para 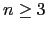 .
.
- Prove que
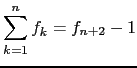 . [Repare que
. [Repare que
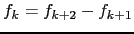 , com
, com
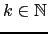 .]
.]
- Use o segundo princípio de indução para mostrar que
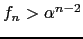 , onde
, onde
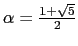 é o número de ouro ou número áureo. [Repare que
é o número de ouro ou número áureo. [Repare que 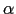 é solução de
é solução de 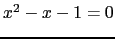 .]
.]
- Mostre que se
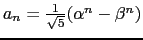 , onde
, onde
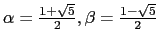 , então
, então
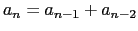 e
e 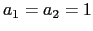 . Conclua que
. Conclua que 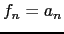 .
.
- Mostre que o quociente da divisão inteira de termos consecutivos da sucessão de Fibonacci é 1.
- Sejam
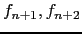 termos consecutivos da sucessão de Fibonacci, com
termos consecutivos da sucessão de Fibonacci, com 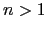 . Mostre que o algoritmo de Euclides tem exactamente
. Mostre que o algoritmo de Euclides tem exactamente 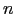 passos para mostrar que
passos para mostrar que
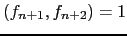 .
.
- Use o algoritmo estendido de Euclides1 para encontrar
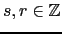 para os quais
para os quais
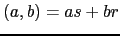 , onde
, onde 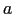 e
e 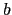 são, respectivamente,
são, respectivamente,
- 45, 75
- 666, 1414
- 102, 222
- 20785, 44350
- 34709, 100313
- 9876543210, 123456789
- 11111111111, 1000000001
- 45666020043321, 73433510078091009
- Implemente uma função no pari/gp que tenha como argumento um natural
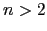 e como retorno a lista dos números primos não superiores a
e como retorno a lista dos números primos não superiores a 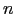 , fazendo uso do crivo de Eratóstenes.
, fazendo uso do crivo de Eratóstenes.
- Implemente uma função no pari/gp que teste a primalidade de um número à custa da divisão trivial.



Seguinte: Sobre este documento ...
2007-03-06
![]() ano
ano
![]() semestre, 2006/2007
semestre, 2006/2007
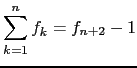 . [Repare que
. [Repare que