- 0-19-853803-
- 3-540-66336-
- 84-9789-613-
- 84-7658-486-
- 972-25-1375-3
- 972-8839-21-9
- 972-8839-06-5
- 972-41-3663-9
- 5601405001101
- 5601522469075
- 5601038100202
- 5601537332739
- 5601370031127
- 8003410344315
- 5000265090209
-
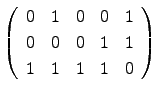 , matriz sobre
, matriz sobre
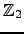 .
.
-
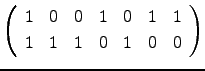 , matriz sobre
, matriz sobre
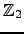 .
.
-
 , matriz sobre
, matriz sobre
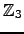 .
.
-
 , matriz sobre
, matriz sobre
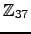 .
.
-
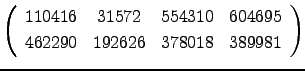 , matriz sobre
, matriz sobre
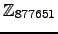 .
.
- crie corpos de Galois
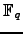 de ordem
de ordem
- matrizes, e determine a nulidade e uma base para o espaço nulo, sobre os corpos da alínea anterior.
-
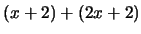 em
em 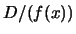 e em
e em 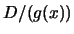 ;
;
-
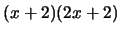 em
em 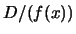 e em
e em 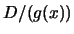 ;
;
- Mostre que
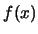 é primitivo em
é primitivo em
![$ {\mathbb{Z}}_3[x]$](img38.png) .
.
- Mostre que
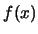 é primitivo em
é primitivo em
![$ {\mathbb{Z}}_5[x]$](img39.png) .
.
- Mostre que
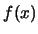 não é primitivo em
não é primitivo em
![$ {\mathbb{Z}}_{11}[x]$](img40.png) .
.
» hamming(3);
![$\displaystyle \left[\begin{array}{ccccccc}
0& 0& 0& 1& 1& 1& 1 \\
0& 1& 1& 0& 0& 1& 1 \\
1& 0& 1& 0& 1& 0& 1 \end{array}\right]$](img57.png)
- r=(1,1,1,1,1,1,1)
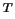 no código
no código ![$ [7,4]$](img59.png) ;
;
- r=(1,0,1,0,1,1,1)
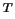 no código
no código ![$ [7,4]$](img59.png) ;
;
- r=(1,0,1,0,1,1,1,0,0,1,1,1,0,0,0)
 , no código
, no código ![$ [15,11]$](img60.png) ;
;
- r=(0,0,1,1,0,0,0,0,1,0,0,0,0,1,0)
 , no código
, no código ![$ [15,11]$](img60.png) ;
;
- r=(1,0,1,0,0,0,1,0,1,1,1,1,0,0,0)
 , no código
, no código ![$ [15,11]$](img60.png) ;
;
- r=(1,1,0,0,1,0,1,1,1,0,0,0,0,0,0)
 , no código
, no código ![$ [15,11]$](img60.png) ;
;
- r=(1,1,0,0,1,1,1,1,1,0,0,1,1,1,1,0,1,1,1,0,1,1,1,0,1,0,0,0,1,1,1)
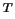 no código
no código ![$ [31,26]$](img61.png) ;
;
- r=(1,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,1,1,1,0,1,0,0,0,0,1,0)
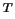 no código
no código ![$ [31,26]$](img61.png) ;
;
- Construa a matriz de paridade e uma matriz geradora do código
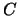 .
.
- Codifique, em
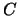 , o vector
, o vector
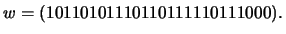
- Corrija os erros e descodifique6 os vectores recebidos:
-
![$ [6,2]$](img70.png) que
seja c.c. 2-erros.
que
seja c.c. 2-erros.
![$ [8,3]$](img71.png) que
seja c.c. 2-erros.
que
seja c.c. 2-erros.
![$ [6,2]$](img70.png) que
seja c.c. 2-erros.
que
seja c.c. 2-erros.
![$ [10,3]$](img72.png) que
seja c.c. 3-erros.
que
seja c.c. 3-erros.
![$ [12,4]$](img73.png) que
seja c.c. 3-erros.
que
seja c.c. 3-erros.
![\begin{displaymath}G_1=\left[\begin{array}{c\vert c}
\begin{array}{cc} 1&1\ 1&1...
...cc} 1&1&0\ 1&1&1\ 1&1&0\ 1&0&1 \end{array}\end{array}\right]\end{displaymath}](img74.png)
- determine o número de elementos do código de que a matriz é geradora;
- indique uma base para o espaço nulo.
- encontre uma matriz de paridade para cada um dos códigos gerados pelas matrizes;
- verifique se os códigos corrigem erros singulares.
(a)
![$ \left[\begin{array}{c\vert c}
I_3 & \begin{array}{ccc} 1&1&0\ 0&1&1\ 1&1&1\end{array}\end{array}\right]$](img75.png) |
(b)
![$ \left[\begin{array}{c\vert c}
I_3 & \begin{array}{ccc} 1&1&1\ 0&1&1\ 1&1&0\end{array}\end{array}\right]$](img76.png) |
(c)
![$ \left[\begin{array}{c\vert c}
I_3 & \begin{array}{ccc} 0&1&1\ 1&1&1\ 1&1&0\end{array}\end{array}\right]$](img77.png) |
(d)
![$ \left[\begin{array}{c\vert c}
I_4 & \begin{array}{cccc} 1&1&0\ 0&1&1\ 1&0&1\ 1&1&1\end{array}\end{array}\right]$](img78.png) |
(e)
![$ \left[\begin{array}{c\vert c}
I_4 & \begin{array}{ccc} 1&1&1\ 0&1&1\ 1&0&1\ 1&1&1\end{array}\end{array}\right]$](img79.png) |
- Considere a relação binária
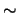 definida am
definida am
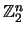 por
por
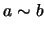 se
se 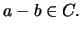
- Verifique se
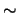 é uma relação de equivalência.
é uma relação de equivalência.
- Mostre que
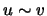 se e só se
se e só se
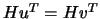 , onde
, onde 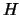 é a
matriz de paridade do código
é a
matriz de paridade do código 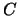 .
.
- Verifique se
- Verifique se a distância de Hamming é uma métrica.
![$ H=\left[\begin{array}{cccccccc}
1&1&1&1&1&1&1&1\\
0&1&0&1&0&1&0&1\\
0&0&1&1&0&0&1&1\\
0&0&0&0&1&1&1&1 \end{array}\right]$](img90.png) a matriz de paridade de um código
linear. Calcule o número de posições corrigíveis nesse código.
a matriz de paridade de um código
linear. Calcule o número de posições corrigíveis nesse código.
![$ G=\left[\begin{array}{cccccc}
1&1&1&0&1&0\\
0&0&1&1&1&1 \end{array}\right]$](img91.png) e suponha que
e suponha que
- Construa o código linear gerado por
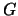 .
.
- Calcule o número de posições corrigíveis.
- Liste os líderes e respectivos síndromes.
- Corrija, se possível,
os vectores recebidos
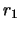 ,
, 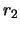 e
e 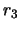 .
.
![$ G=\left[\begin{array}{cccccc}
1&1&0&0&1&1\\
0&0&1&0&1&1 \end{array}\right]$](img97.png) é a matriz geradora de um código linear
é a matriz geradora de um código linear - os parâmetros
![$ [n,k]$](img80.png) ;
;
- a matriz de paridade;
- a distância mínima do código e o número de posições corrigíveis;
- a correcção dos vectores recebidos
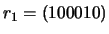 e
e
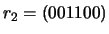 .
.
![$ G=\left[\begin{array}{cccccc }
1&0 &0&1&1&0\\
0&1 &0&1&0&1\\
0&0&1&0&1&0 \end{array}\right]$](img101.png) .
.
- Encontre a matriz de paridade
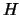 de
de 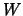 e os parâmetros
e os parâmetros
![$ [n,k,d]$](img103.png) .
.
- Verifique se
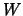 é auto-dual.
é auto-dual.
- Corrija os vectores recebidos
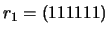 e
e
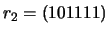
![\begin{displaymath}\left[\begin{array}{c\vert c}
I_4 &
\begin{array}{ccc}
1 & 0 ...
... 0 & 1\\
0 & 1 & 1\\
0 & 1 & 1
\end{array}\end{array}\right].\end{displaymath}](img106.png)
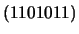 ;
;
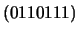 ;
;
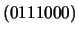 .
.
![$ H=\left[\begin{array}{ccc}
?&1&0\\
?&0&1\end{array}\right]$](img110.png) de forma a que seja a matriz de paridade de uma código
linear com correcção de 1 bit.
de forma a que seja a matriz de paridade de uma código
linear com correcção de 1 bit.
- mostre, via MuPad, que
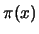 é irredutível
é irredutível
- mostre que
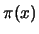 é primitivo
é primitivo
- usando matrizes;
- via MuPad.
- Para cada um dos polinómios em
![$ {\mathbb{Z}}_ 2[x]$](img42.png) apresentados,
construa, se possível, o código BCH e os respectivos parâmetros
apresentados,
construa, se possível, o código BCH e os respectivos parâmetros
![$ [n,k,d]$](img103.png) e número de p.c.:
e número de p.c.:
-
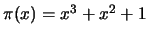 c.c. 1-erro,
c.c. 1-erro,
-
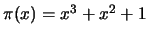 c.c. 2-erros,
c.c. 2-erros,
-
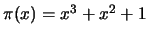 c.c. 3-erros,
c.c. 3-erros,
-
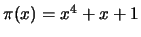 de forma a que seja
de forma a que seja ![$ [15,7]$](img115.png) ,
,
-
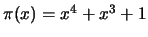 c.c. 2-erros,
c.c. 2-erros,
-
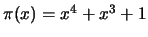 c.c. 3-erros,
c.c. 3-erros,
-
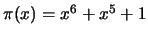 c.c. 3-erros.
c.c. 3-erros.
-
- Seja
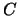 o código BCH obtido do polinómio primitivo
o código BCH obtido do polinómio primitivo
![$ \pi(x)=x^4+x+1\in {\mathbb{Z}}_2[x]$](img111.png) , considerando as primeiras 6 potências
de
, considerando as primeiras 6 potências
de 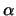 . Corrija, em
. Corrija, em 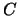 , os seguintes vectores recebidos por um
canal com ruído:
, os seguintes vectores recebidos por um
canal com ruído:
-
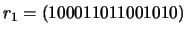 ;
;
-
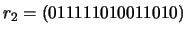 ;
;
-
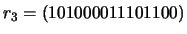 ;
;
-
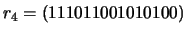 .
.
-
- Mostre que
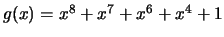 é polinómio gerador de
é polinómio gerador de 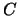 .
.
- Corrija, em
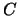 , o seguinte vector recebido por um
canal com ruído:
, o seguinte vector recebido por um
canal com ruído:
![$\displaystyle r=\left[\begin{array}{ccccccccccccccc}
1 & 0 &1 &1 &0 &0 &1 &1 &1 & 0&0&1&0&0&0\end{array}\right].$](img124.png)
- Verifique que
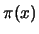 é primitivo.
é primitivo.
- Encontre os polinómios minimais aniquiladores das 6 primeiras
potências de
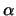 .
.
- Seja
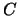 o código BCH obtido do polinómio primitivo
o código BCH obtido do polinómio primitivo 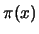 corrector de 2 erros. Corrija, em
corrector de 2 erros. Corrija, em 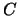 , o seguinte vector recebido por um
canal com ruído:
, o seguinte vector recebido por um
canal com ruído:
![$\displaystyle r=\left[\begin{array}{ccccccccccccccc}
1 & 0 &1 &0 &1 &0 &0 &0 &1 & 0&0&0&0&0&0\end{array}\right].$](img126.png)
- Codifique, em
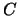 , o vector
apresentando o resultado final como um vector linha sobre
, o vector
apresentando o resultado final como um vector linha sobre![$\displaystyle r=\left[\begin{array}{ccccccc}
1 & 0 &0 &1 &0 &0 &0 \end{array}\right],$](img127.png)
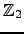 .
.
- Corrija, em
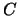 , o seguinte vector recebido por um
canal com ruído:
, o seguinte vector recebido por um
canal com ruído:
![$\displaystyle r=\left[\begin{array}{ccccccccccccccc}
0 & 0 &0 &0 &1 &0 &1 &0 &1 & 1&1&1&0&0&0\end{array}\right].$](img128.png)