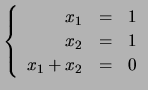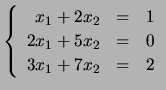-
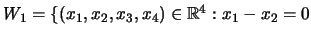 e
e
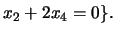
-
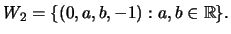
-
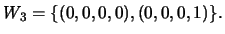
-
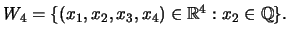
![]()
![]()
![]()
![]() ,
,
![]() .
.
Verifique se
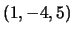 é combinação linear de
é combinação linear de
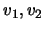 .
.
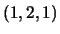 é combinação linear de
é combinação linear de
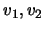 .
.
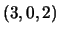 é combinação linear de
é combinação linear de
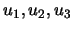 .
.
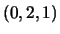 é combinação linear de
é combinação linear de
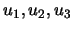 .
.
-
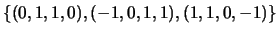 no espaço vectorial real
no espaço vectorial real
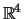 .
.
-
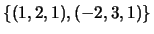 no espaço vectorial real
no espaço vectorial real
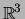 .
.
-
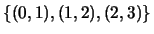 no espaço vectorial real
no espaço vectorial real
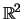 .
.
-
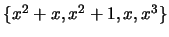 no espaço vectorial real
no espaço vectorial real
![$ \mathbb{R}%%
_{3}[x]$](img28.png) .
.
-
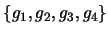 no espaço vectorial real
no espaço vectorial real
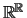 onde
onde
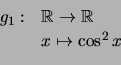 ,
,
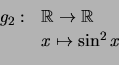 ,
,
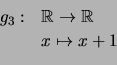 ,
,
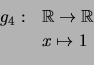
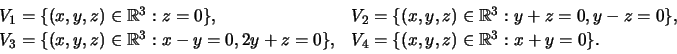
![]()
Indique a dimensão e uma base para cada um deles.
![]()
![]()
![]() .
.
- Diga, justificando, se
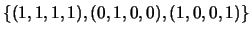 é uma
base de
é uma
base de 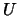 .
.
- Determine uma base de i.
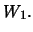 ii.
ii. 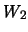 .
.
![]()
![]() ,
,
![]() .
.
- Determine os valores do parâmetro real
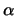 para os quais o
conjunto
para os quais o
conjunto
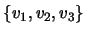 é uma base de
é uma base de
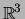 .
.
- Para um dos valores de
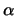 determinados na alínea anterior,
calcule as coordenadas do vector
determinados na alínea anterior,
calcule as coordenadas do vector
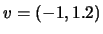 em relação à base
em relação à base
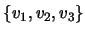 .
.
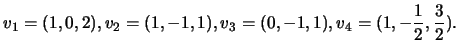
- Mostre que são uma base de
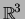 .
.
- Determine as coordenadas de
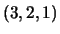 relativamente a esta base.
relativamente a esta base.
-
![$ \left[\begin{array}{ccc}2 & 8 & -2\\
1 &-17 & 6\\
9 & 6 & 1\end{array}\right]$](img67.png)
-
![$ \left[\begin{array}{cccc} 3 & -4 &0 &4\\
2 & 4 &-2 & 0\\
3 &-2 &4 &-4\end{array}\right]$](img68.png) .
.
-
![$ \left[\begin{array}{ccccc} 0 &-7 & 3 & -8 & -1\\
-1 & 6 &-8 &-2 & 3\\
0 & 0 & 0 & 5 & -8\end{array}\right]$](img69.png)
``Se as colunas da matriz quadrada ![]() são linearmente
independentes, então as colunas de
são linearmente
independentes, então as colunas de ![]() são também elas
linearmente independentes.''
são também elas
linearmente independentes.''
- se
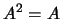 e
e 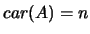 então
então 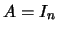 ;
;
- se
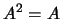 então
então
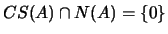 .
.
![$ A=\left[\begin{array}{ccc} 1& -3& 2\\ 4 & 10 & -1\end{array}\right]^T$](img79.png) e
e
![$ b= \left[\begin{array}{ccc}5&7&10\end{array}\right]^T$](img80.png) , determine a solução no sentido dos mínimos quadrados de
, determine a solução no sentido dos mínimos quadrados de
![$ A=\left[\begin{array}{cc}
1&1\\
1 & 0\\
0 & 1\\
1 & 1 \end{array}\right]$](img84.png) .
.
- Calcule a projecção ortogonal de
![$ b=\left[\begin{array}{cccc}
4&5&-1&4 \end{array}\right]^T$](img85.png) sobre
sobre 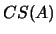 .
.
- O que pode dizer sobre o sistema
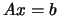 ?
?