A=fix(30*rand(3,3)-15);Responda às alíneas seguintes para várias escolhas de
- Descreva o output de Ainf=tril (A) e de Asup=triu (A)
- Calcule e comente o resultado de det(Ainf) e de det(Asup).
- Troque duas linhas de
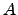 e compare o determinante da matriz obtida com
e compare o determinante da matriz obtida com 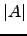 . Repita o exercício fazendo trocas de colunas.
. Repita o exercício fazendo trocas de colunas.
- Substitua uma linha/coluna de
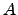 pela linha nula e calcule o determinante da matriz obtida.
pela linha nula e calcule o determinante da matriz obtida.
- Multiplique uma linha por um escalar não nulo e compare o determinante da matriz obtida com
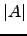 . Repita o exercício multiplicando uma coluna por um escalar não nulo.
. Repita o exercício multiplicando uma coluna por um escalar não nulo.
- A uma linha de
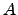 some-lhe outra multiplicada por um escalar não nulo. Compare o determinante da matriz obtida com
some-lhe outra multiplicada por um escalar não nulo. Compare o determinante da matriz obtida com 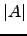 . Repita o exercício fazendo a operação elementar por colunas.
. Repita o exercício fazendo a operação elementar por colunas.
- Use [L,U,P]=lu (A) para obter a factorização
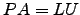 . Compare
. Compare 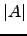 com
com 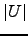 .
.
- O que pode conjecturar sobre a relação entre
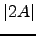 e
e 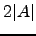 ? Teste a validade da sua conjectura.
? Teste a validade da sua conjectura.
- Introduza os comandos
[l,u,p]=lu (B) u(1,1)*u(2,2)*u(3,3) u(1,1)*u(2,2)*u(3,3)-det(B)
Interprete os comandos introduzidos e os resultados obtidos. - Repita a alínea anterior para as matrizes
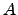 e
e 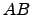 .
.
- Compare
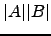 e
e 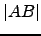 .
.
- Verifique que
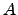 é não singular. Relacione
é não singular. Relacione 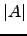 com
com 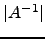 .
.
- Verifique se
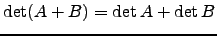 .
.
- Verifique que
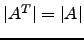 .
.
- Mostre que
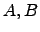 são não-singulares.
são não-singulares.
- Compare
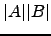 e
e 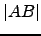 .
.
- Relacione
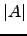 com
com 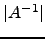 .
.
- Relacione
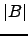 com
com 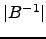 .
.
- Considere
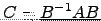 . Compare
. Compare 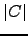 com
com 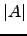 . Que resultado pode conjecturar?
. Que resultado pode conjecturar?
- Verifique se
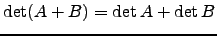 .
.
- Verifique que
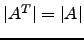 e que
e que 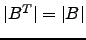 .
.
> R=fix(-10+rand(7)*20); > S=fix(-10+rand(7)*20); > P=fix(-10+rand(4)*20);
- Calcule e compare, para várias escolhas,
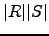 e
e  . O que pode inferir?
. O que pode inferir?
- Calcule e compare, para várias escolhas,
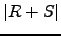 e
e 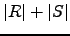 . O que pode concluir?
. O que pode concluir?
- para C=[ -0 -3 3 4; 0 -1 -0 -3; 2 -4 -4 -0; -4 -2 1 -4];, determine
C*adjunta(C)/det(C); que pode observar? - para A=[ 2 2 -0 -3; 2 -0 -1 -2; 4 -3 -1 4; -3 0 4 -1];, determine
A*adjunta(A); que pode observar? - para B=[ -2 3 -2 2; -4 3 -1 2; -2 -4 3 -1; 3 -1 3 -2];, determine
B*adjunta(B); o que pode observar?
(a)
![$ \left[\begin{array}{cc} 5 & 2 7 & 3\end{array}\right]$](img24.png) |
(b)
![$ \left[\begin{array}{cc} 1 & 2 3 & 4\end{array}\right]$](img25.png) |
(c)
![$ \left[\begin{array}{cc} 3 & 2 8 & 5\end{array}\right]$](img26.png) |
(d)
![$ \left[\begin{array}{cc} 6 & 9 8 & 12\end{array}\right]$](img27.png) |
(e)
![$ \left[\begin{array}{cc} a^2 & ab ab & b^2\end{array}\right]$](img28.png) |
(f)
![$ \left[\begin{array}{cc} n+1 & n n & n-1\end{array}\right]$](img29.png) |
(g)
![$ \left[\begin{array}{cc} a+b & a-b a-b & a+b\end{array}\right]$](img30.png) |
(h)
![$ \left[\begin{array}{cc} 1 & \text{i} 1 & \i\end{array}\right]$](img31.png) |
(i)
![$ \left[\begin{array}{cc} a & c+d \text{i} c-d \text{i}& b\end{array}\right]$](img32.png) |
(j)
![$ \left[\begin{array}{cc} a+b \text{i}& b 2a & a-b \text{i}\end{array}\right]$](img33.png) |
(k)
![$ \left[\begin{array}{cc} \cos \alpha & -\sin \alpha \sin \alpha & \cos \alpha \end{array}\right]$](img34.png) |
(l)
![$ \left[\begin{array}{cc} 1 & \text{i} - \text{i}& 1\end{array}\right]$](img35.png) |
-
![$ \left[\begin{array}{ccc} 1 & 0 & 0 5 & 1 & 2 7 & 1 & 1\end{array}\right]$](img36.png) .
.
-
![$ \left[\begin{array}{ccc} 0 & 1 & 2 2 & 1 & 1 2 & 3 & 3\end{array}\right]$](img37.png) .
.
-
![$ \left[\begin{array}{cccc} 0 & 0 & 1 & 1 1 & 5 & 1 & 2 0&1&1&1 0 & 0 & 0 & 1\end{array}\right]$](img38.png) .
.